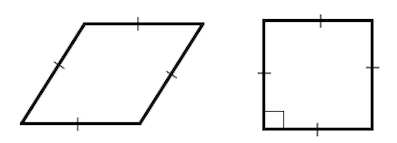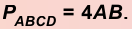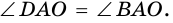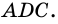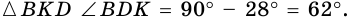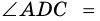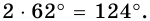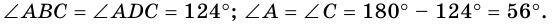как доказать что это ромб
Ромб. Свойства и признаки ромба
Ромб – это параллелограмм, у которого все стороны равны.
Если у ромба – прямые углы, то он называется квадратом.
Свойства ромба
1. Поскольку ромб – это параллелограмм, то все свойства параллелограмма верны для ромба.
Помимо этого:
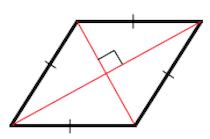
2. Диагонали ромба перпендикулярны.
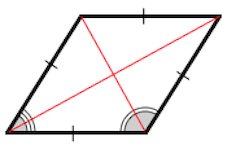
3. Диагонали ромба являются биссектрисами его углов.
4. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
Признаки ромба
Чтобы параллелограмм оказался ромбом, необходимо выполнение одного из следующих условий:
1. Все стороны параллелограмма равны между собой ().
2. Диагонали пересекаются под прямым углом ().
3. Диагонали параллелограмма являются биссектрисами его углов.
Площадь ромба
Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Что такое ромб: определение, свойства, признаки
В данной публикации мы рассмотрим определение, свойства и признаки (с рисунками) одной из основных геометрических фигур – ромба.
Определение ромба
Ромб – это фигура на плоскости; разновидность параллелограмма, у которого все четыре стороны равны и попарно параллельны. Обычно ромб обозначается названиями его вершин (например, ABCD), а длина его стороны – строчной латинской буквой (например, a).
Примечание: квадрат является частным случаем ромба.
Свойства ромба
Свойство 1
Противоположные углы ромба равны между собой, а сумма соседних углов составляет 180°.
Свойство 2
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
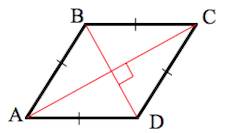
В результате пересечения диагоналей ромб делится на 4 прямоугольных треугольника: ΔAEB, ΔBEC, ΔAED и ΔDEC.
Свойство 3
Диагонали ромба являются биссектрисами его углов.
Свойство 4
Сторону ромба a можно найти через его диагонали d1 и d2 (согласно теореме Пифагора).
Свойство 5
В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
Радиус вписанной в ромб окружности r вычисляется по формуле:
Признаки ромба
Параллелограмм является ромбом только в том случае, если для него верно одно из следующих утверждений:
Примечание: Любой четырехугольник, стороны которого равны, является ромбом.
Ромб и его свойства, определение и примеры с решением
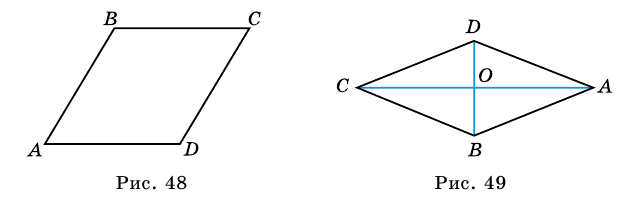
Ромбом называют параллелограмм, у которого все стороны равны (рис. 48).
Так как ромб является параллелограммом, то он имеет все свойства параллелограмма.
1. Сумма любых двух соседних углов ромба равна 180°.
2. У ромба противолежащие углы равны.
3. Диагонали ромба точкой пересечения делятся пополам.
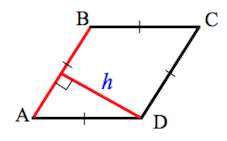
4. Периметр ромба
Кроме того, ромб имеет еще и такое свойство.
5. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Доказательство:
Пусть 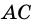
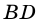
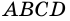
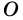
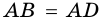
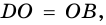
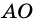
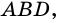
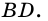
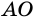
Следовательно, 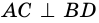
Аналогично можно доказать, что диагональ АС делит пополам угол 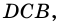
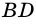
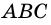
Пример:
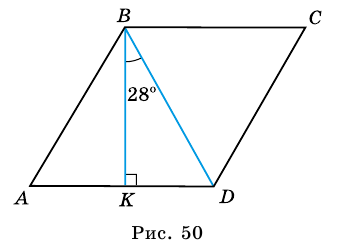
Угол между высотой и диагональю ромба проведенными из одной вершины, равен 28°. Найдите углы ромба.
Решение:
Пусть 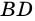
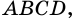
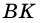
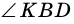
1) В
2) Так как 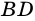
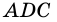
3) Тогда
Ответ. 124°, 56°, 124°, 56°.
Рассмотрим признаки ромба.
Теорема (признаки ромба). Если в параллелограмме: 1) две соседние стороны равны, или 2) диагонали пересекаются под прямым углом, или 3) диагональ делит пополам углы параллелограмма, — то параллелограмм является ромбом.
Доказательство:
1) Пусть 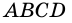
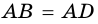
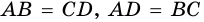
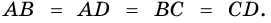
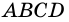
2) Пусть 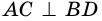
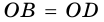
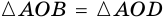
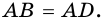
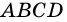
3) Диагональ 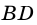
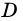
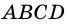
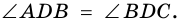
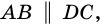
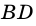
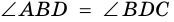
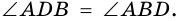
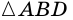
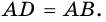
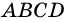
Пример:
Доказательство:
Пусть 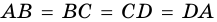
1) Так как противолежащие стороны четырехугольника 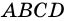
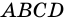
2) У параллелограмма 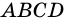
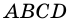
Слово «ромб» греческого происхождения, которое в древние времена означало вращающееся тело, веретено, волчок. Ромб тогда связывали с сечением веретена, на которое намотаны нити.
В «Началах» Евклида термин «ромб» встречается единожды, а свойства ромба Евклид вообще не рассматривал.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Как доказать что это ромб
Ромб — это четырехугольник, имеющий равные длины сторон.
Ромб является частным случаем параллелограмма.
Ромб имеющий прямые углы является квадратом.
Содержание
Свойства ромба
1. Противолежащие стороны ромба параллельны и равны.
AB \parallel CD,\;BC \parallel AD
2. Диагонали ромба перпендикулярны.
Так как ромб является параллелограммом, то его диагонали делятся пополам.
\Rightarrow \angle BOC = 90^ <\circ>и \angle COD = 90^ <\circ>.
3. Точка пересечения диагоналей делит их пополам.
AC=2\cdot AO=2\cdot CO
BD=2\cdot BO=2\cdot DO
4. Диагонали ромба являются биссектрисами его углов.
\angle 1 = \angle 2; \; \angle 5 = \angle 6 ;
По причине того, что диагонали разделены точкой пересечения пополам, и все стороны ромба равны друг другу, то вся фигура делится диагоналями на 4 равных треугольника:
5. Диагонали образуют из ромба 4 прямоугольных треугольника.
6. Любой ромб может содержать окружность с центром в точке пересечения его диагоналей.
7. Сумма квадратов диагоналей равна квадрату одной из сторон ромба умноженному на четыре
AC^2 + BD^2 = 4\cdot AB^2
Признаки ромба
1. Параллелограмм с перпендикулярными диагоналями является ромбом.
\begin
2. Когда в параллелограмме хотя бы одна из диагоналей разделяет оба угла (через которые она проходит) пополам, то этой фигурой будет ромб.
Следовательно, \triangle ABC = \triangle ADC и оби фигуры — равнобедренные треугольники.
На заметку: не каждая фигура (четырехугольник) с перпендикулярными диагоналями будет ромбом.
Это уже не ромб, не смотря на перпендикулярность диагоналей.
Для отличия стоит запомнить, что сначала четырехугольник должен быть параллелограммом и иметь признаки параллелограмма 1 и 2
Ромб, его свойства и признаки.
Ромб, его свойства и признаки.
Рассмотрим ещё два вида параллелограмма.
Определение. Ромбом называется параллелограмм, у которого все стороны равны.
Поскольку ромб является параллелограммом, то он обладает теми же свойствами, что и параллелограмм, т.е.: у ромба противолежащие углы равны (стороны у него и так все равны, поэтому в этом свойстве мы опускаем равенство противолежащих сторон); диагонали ромба пересекаются и точкой пересечения делятся пополам. Кроме того, ромб обладает ещё и своими, особенными свойствами. Рассмотрим их.
ТЕОРЕМА. У ромба диагонали взаимно перпендикулярны.
2. и – смежные, значит, по свойству смежных углов
, как, впрочем, и остальные углы (мы знаем, что если угол прямой, то смежный с ним угол также прямой).
3. Итак, прямые и при пересечении образуют прямой угол, значит, эти прямые перпендикулярны, т.е. , ч.т.д.
ТЕОРЕМА. У ромба диагонали являются биссектрисами углов.
Доказать: – биссектриса и
Для того, чтобы доказать, что и являются биссектрисами углов, нам нужно доказать, что они делят эти углы пополам.
Итак, ромб обладает следующими свойствами :
У ромба диагонали пересекаются и точкой пересечения делятся пополам.
У ромба диагонали взаимно перпендикулярны.
У ромба диагонали являются биссектрисами его углов.
У ромба противоположные углы равны.
У ромба высоты равны.
Теперь определим признаки ромба.
ТЕОРЕМА ( I признак ромба). Если у параллелограмма две смежные стороны равны, то такой параллелограмм является ромбом.
Так как – параллелограмм, то у него противолежащие стороны равны.
– ромб (по определению), ч.т.д.
ТЕОРЕМА ( II признак ромба). Если у параллелограмма диагонали взаимно перпендикулярны, то такой параллелограмм является ромбом.
по свойству диагоналей параллелограмма, значит, – медиана (по опред-нию).
ТЕОРЕМА ( III признак ромба). Если у параллелограмма диагональ является биссектрисой его угла, то этот параллелограмм является ромбом.
ТЕОРЕМА ( IV признак ромба). Если у параллелограмма высоты равны, то такой параллелограмм является ромбом.
ТЕОРЕМА ( V признак ромба). Если в четырёхугольнике все стороны равны, то он является ромбом.
Если у параллелограмма две смежные стороны равны, то такой параллелограмм является ромбом.
Если у параллелограмма диагонали взаимно перпендикулярны, то такой параллелограмм является ромбом.
Если у параллелограмма диагональ является биссектрисой его угла, то этот параллелограмм является ромбом.
Если у параллелограмма высоты равны, то такой параллелограмм является ромбом.
Если в четырёхугольнике все стороны равны, то он является ромбом.
Сторона ромба равна см. Найдите периметр ромба.
Найдите все углы ромба, если его сторона равна диагонали.
Найдите углы ромба, если основание перпендикуляра, опущенного из вершины тупого угла, делит сторону ромба пополам.
Периметр ромба равен см, расстояние между противолежащими сторонами равно см. Найдите углы ромба.
Найдите углы ромба, если его диагонали составляют с его стороной углы, один из которых на меньше другого.
Докажите, что точка пересечения диагоналей ромба равноудалена от его сторон.
Докажите, что параллелограмм, у которого две смежные стороны равны, является ромбом.
Докажите, что если каждая диагональ четырёхугольника делит пополам два его угла, то этот четырёхугольник является ромбом.
Через точку пересечения диагоналей ромба проведены перпендикуляры к его сторонам. Докажите, что точки пересечения этих перпендикуляров со сторонами ромба являются вершинами прямоугольника.
В параллелограмме биссектрисы углов и пересекают стороны параллелограмма и в точках и соответственно. Докажите, что четырёхугольник – ромб.
В ромбе перпендикуляр, проведённый из вершины тупого угла к стороне ромба, делит эту сторону пополам. Найдите углы ромба.
Докажите, что четырёхугольник, вершины которого находятся в серединах сторон прямоугольника, является ромбом.
Периметр ромба равен см. Найдите сторону ромба.
Два ромба имеют общую точку пересечения диагоналей, причём, меньшие диагонали этих ромбов взаимно перпендикулярны. Докажите, что прямая, проходящая через точку пересечения диагоналей и середину стороны одного ромба, перпендикулярна стороне другого.
Найдите величину большего угла ромба, если его сторона равна одной из его диагоналей.
Докажите, что треугольник равнобедренный.
В ромбе биссектриса угла делит сторону ромба пополам. Найдите тупой угол ромба.