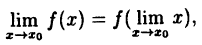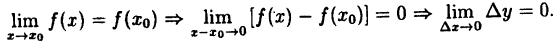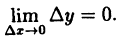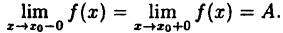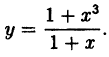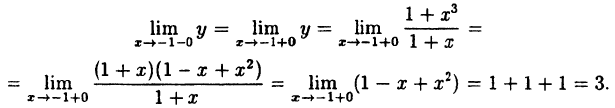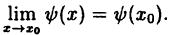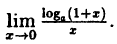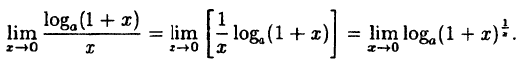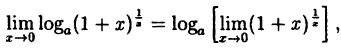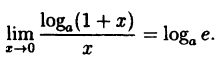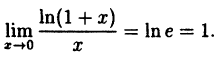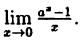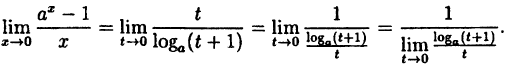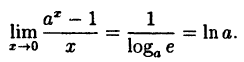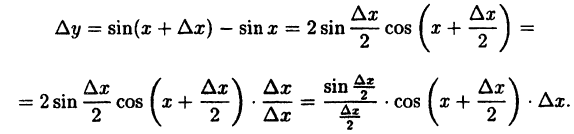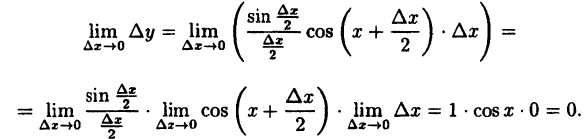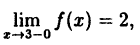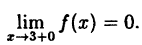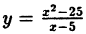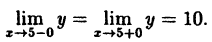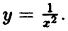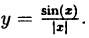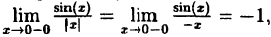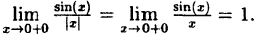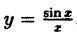как доказать что функция непрерывна
Как доказать непрерывность функции
Пример 1: докажите непрерывность функции f(x) = x^2 в точке x_0.
По ε-Δ определению существует такое ε > 0, что |x^2 – x_0^2|
Некоторые элементарные функции являются непрерывными на всей области определения (множестве значений X):
Пример 2: докажите непрерывность функции f(x) = sin x.
По определению непрерывности функции по ее бесконечно малому приращению запишите:
Преобразуйте по формуле для тригонометрических функций:
Δf = 2*cos((x + Δx)/2)*sin(Δx/2).
Функция cos ограничена при x ≤ 0, а предел функции sin(Δx/2) стремится к нулю, следовательно, она является бесконечно малой при Δx→0. Произведение ограниченной функции и бесконечно малоq величины, а значит и приращение исходной функции Δf также является бесконечной малой величиной. Следовательно, функция f(x) = sin x непрерывна для любого значения x.
Пример 1: докажите непрерывность функции f(x) = x^2 в точке x_0.
По ε-Δ определению существует такое ε > 0, что |x^2 – x_0^2|
Некоторые элементарные функции являются непрерывными на всей области определения (множестве значений X):
Пример 2: докажите непрерывность функции f(x) = sin x.
По определению непрерывности функции по ее бесконечно малому приращению запишите:
Преобразуйте по формуле для тригонометрических функций:
Δf = 2*cos((x + Δx)/2)*sin(Δx/2).
Функция cos ограничена при x ≤ 0, а предел функции sin(Δx/2) стремится к нулю, следовательно, она является бесконечно малой при Δx→0. Произведение ограниченной функции и бесконечно малоq величины, а значит и приращение исходной функции Δf также является бесконечной малой величиной. Следовательно, функция f(x) = sin x непрерывна для любого значения x.
Некоторые элементарные функции являются непрерывными на всей области определения (множестве значений X):
Пример 2: докажите непрерывность функции f(x) = sin x.
По определению непрерывности функции по ее бесконечно малому приращению запишите:
Преобразуйте по формуле для тригонометрических функций:
Δf = 2*cos((x + Δx)/2)*sin(Δx/2).
Функция cos ограничена при x ≤ 0, а предел функции sin(Δx/2) стремится к нулю, следовательно, она является бесконечно малой при Δx→0. Произведение ограниченной функции и бесконечно малоq величины, а значит и приращение исходной функции Δf также является бесконечной малой величиной. Следовательно, функция f(x) = sin x непрерывна для любого значения x.
Непрерывность функций с примерами решения и образцами выполнения
Непрерывность функции:
Непрерывные функции, точки разрыва и их классификация, действия над непрерывными функциями, свойства функций, непрерывных на сегменте.
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если:
Если в точке x₀ функция непрерывна, то точка x₀ называется точкой непрерывности функции.
Пример:
Исследовать на непрерывность функцию 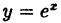
Решение:
Чтобы доказать, что функция 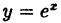
Таким образом, доказано, что функция 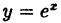
Замечание:
Формулу (10.1) можно записать в виде
(10.2)
так как 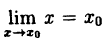
Введем понятие непрерывности функции в точке х₀ справа и слева.
Если, существует 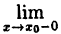
Так как ∆x = x-x₀, a ∆y = f(x)-(x₀), то условие (10.1) равносильно следующему:
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции
(10.3)
Пример:
Показать, что функция у = х³ непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y.
Используя теоремы о пределе суммы и произведения функции, получим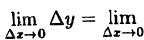
Следовательно, функция у = х³ непрерывна при — ∞ Точки разрыва функции и их классификация
Определение:
Точка х₀ называется точкой разрыва функции у = f(x), если она принадлежит области определения функции или ее границе и не является точкой непрерывности.
Так, например, функция 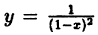
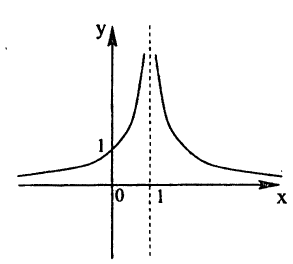
Определение:
Точка разрыва x₀ функции у = f(x) называется точкой устранимого разрыва, если существуют оба односторонних предела в точке x₀ и они равны, т. е.
Пример:
Исследовать на непрерывность функцию
Решение:
В точке x=-1 функция не определена, так как, выполнив подстановку, получаем неопределенность 
Определение:
Если в точке x₀ односторонние пределы слева и справа существуют, но не равны, точка x₀ называется точкой разрыва I рода.
Пример:
Исследовать на непрерывность функцию
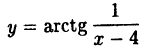
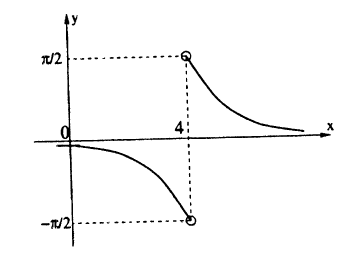
Решение: Вычислим односторонние пределы функции в точке ее разрыва х = 4.
Предел слева —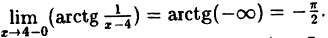
Предел справа — 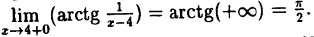
Пределы слева и справа существуют, но не равны, следовательно, точка x = 4 для данной функции — точка разрыва I рода (точка скачка).
Определение:
Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода.
В точках разрыва II рода не существует хотя бы один из односторонних пределов. Функция 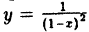
Действия над непрерывными функциями
Теорема:
Непрерывность суммы, произведения и частного непрерывных функций. Если функции ϕ(x) и ψ(x) непрерывны в точке Хо, то их сумма и произведение также непрерывны в точке x₀. Если, кроме того, знаменатель в рассматриваемой точке не равен нулю, то частное непрерывных функций есть функция непрерывная.
Докажем непрерывность произведения.
Дано: непрерывность функций в точке x₀:
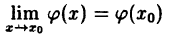
Доказать, что f(x) — ϕ(x) ∙ ψ(x) есть функция непрерывная в точке x₀, т. е. 
Доказательство:




Можно строго доказать, что все основные элементарные функции непрерывны при всех значениях х, для которых они определены.
Например, степенная у = xⁿ, показательная у = 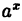
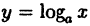
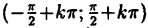
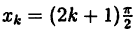
Теорема:
Непрерывность сложной функции. Если функция и = ϕ(x) непрерывна в точке x₀, а функция у = f(u) непрерывна в точке и₀ = ϕ(x₀), то сложная функция у = f [ϕ(x)] непрерывна в точке x₀.
В заключение этого раздела рассмотрим два предела, которые нам понадобятся в дальнейшем.
Пример:
Вычислить
Решение:
Заметим, что при х → 0 числитель и знаменатель одновременно стремятся к нулю, т.е. имеет место неопределенность вида 
Так как данная логарифмическая функция непрерывна в окрестности точки х = 0, то можно перейти к пределу под знаком функции ( 

но 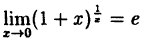
Следовательно,
(10.4)
В частности, при а = е
(10.5)
Таким образом, у = ln( 1 + х) и у = х — эквивалентные бесконечно малые функции при х → 0.
Пример:
Вычислить
Решение:
Здесь мы имеем дело с неопределенностью вида 
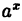
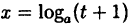
Так как на основании результата, полученного в предыдущем примере, 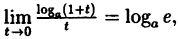
(10.6)
В частности, если а = е, имеем
т.е. у = 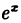
Свойства функций, непрерывных на сегменте
Определение:
Функция у = f(x) непрерывна на сегменте [а, b], если она непрерывна во всех внутренних точках Этого сегмента, а на концах сегмента (в точках a и b) непрерывна соответственно справа и слева.
Теорема:
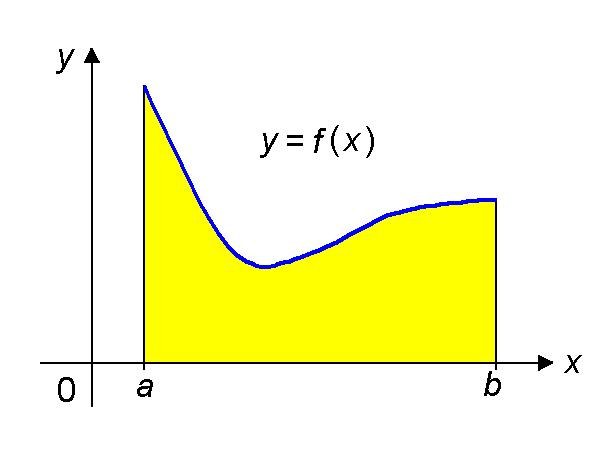
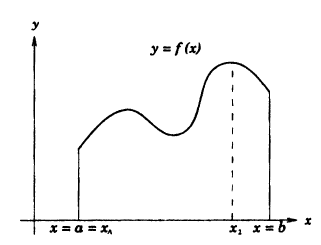
Если функция у = f(x) непрерывна на сегменте [а, b], то она достигает на этом сегменте своего наибольшего и(или) наименьшего значения.
Простым доказательством этой теоремы, является геометрическая иллюстрация функции у = f(x) на рисунке 91. Непрерывная на сегменте [α, b] функция достигает наименьшего своего значения в точке х = x₁= а, а наибольшего значения в точке х₂.
Следствие:
Если функция у = f(x) непрерывна на сегменте [a, b], то она ограничена на этом сегменте.
Действительно, если по теореме 10.3 функция достигает на сегменте наибольшего M и наименьшего т значений, то имеет место неравенство m ≤ f(x) ≤ M для всех значений функции на рассматриваемом сегменте. Т. е. |f(x)| ≤ M и, следовательно, функция у = f(x) ограничена на сегменте [а, b].
Теорема:
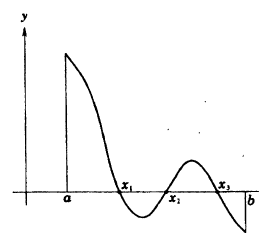
Теорема Больцано-Коши. Если функция у = f(x) непрерывна на сегменте [а, b] и на ее концах принимает значения разных знаков, то внутри этого сегмента найдется, по крайней мере, одна тонка С, в которой функция равна нулю.
Геометрический смысл теоремы заключается в следующем: если точки графика функции у = f(x), соответствующие концам сегмента [a, b], лежат по разные стороны от оси ОХ, то этот график хотя бы в одной точке сегмента пересекает ось OX. На данном рисунке 92 это три точки x₁, x₂, x₃.
Теорема:
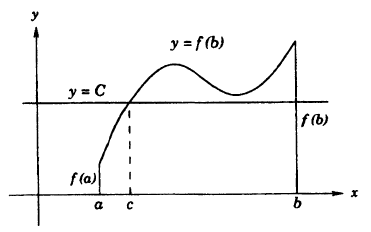
О промежуточных значениях функции. Если функция у = f(x) непрерывна на сегменте [α, b] и f(α) = A и f(b) = В, то для любого числа С, заключенного между A и B, найдется внутри этого сегмента такая точка с, что f(c) = С.
Из графика на рисунке 93 видно, что непрерывная функция, переходя от одного значения к другому, обязательно проходит через все промежуточные значения.
Теорема:
О непрерывности обратной функции.) Если функция у = f(x) непрерывна на сегменте [а, b] в возрастает (убывает) на этом сегменте, то обратная функция х = f⁻¹(y) на соответствующем сегменте оси OY существует и является также непрерывной возрастающей (убывающей) функцией.
Эту теорему мы принимаем без доказательства.
Решение на тему: Непрерывная функция
Пример:
Показать, что функция у = 4x² непрерывна в точке х = 2.
Решение:
Для этого необходимо показать, что в точке х = 2 выполняется все три условия непрерывности функции:
1) функция у = 4х² определена в точке х = 2 ⇒ f(2) = 16;
2) существует 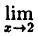
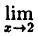
3) этот предел равен значению функции в точке х = 2
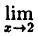
Пример:
Показать, что функция у = sin x непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y, используя формулы тригонометрических тождеств
Так как 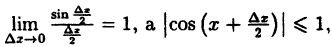
Эта функция (рис. 94) определена во всех точках сегмента [0,4] и ее значение при х = 3 ⇒ у = 2. Функция терпит разрыв, так как она не имеет предела при х → 3 :
Следовательно, точка х = 3, точка разрыва первого рода. При этом в граничных точках исследуемого сегмента [0,4], функция f(x) непрерывна справа (х = 0) и непрерывна слева (х = 4).
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 5 функция не определена, т.к., выполнив подстановку, получаем неопределенность вида 0/0. Легко доказать, что
Следовательно, точка х = 5 точка устранимого разрыва.
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 0 функция (рис. 95) терпит разрыв, так как она не определена в этой точке. Пределы функции слева и справа от точки х = 0 равны ∞. Следовательно, точка х = 0 для данной функции является точкой разрыва второго
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 0 функция терпит разрыв 1-го рода, так как односторонние пределы существуют в этой точке, но не равны:
предел слева
предел справа
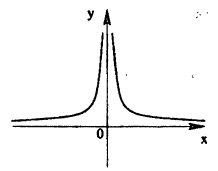
Пример:
Исследовать на непрерывность функцию 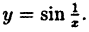
Решение:
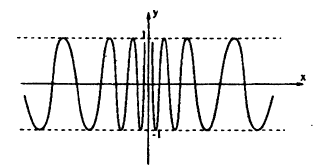
Пример:
Исследовать на непрерывность функцию
Решение:
Функция 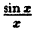
Если доопределить функцию 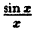
f(х) =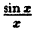
Доопределив функцию в точке х = 0, мы устранили разрыв.
Непрерывность функций



Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Как доказать что функция непрерывна
Пусть функция `y=f(x)` определена на некотором интервале, содержащем точку `ain R`, за исключением, быть может, самой точки `a`.
Число `A` называется пределом функции `y=f(x)` в точке `a`, если для любой последовательности `(x_n)` из области её определения такой, что `x_n!=a` и `lim_(n->oo)x_n=a` выполняется равенство `lim_(n->oo)f(x_n)=A`.
Обозначение: `lim_(n->oo)f(x)=A`, или `f(x)->A` при `x->a`.
В определении предела рассматриваются значения `x_n`, не равные `a`, поэтому в самой точке `a` функция `y=f(x)` может быть не определена; если значение `f(a)` определено, то оно не обязано совпадать с `A`. К тому же, поскольку последовательность `(f(x_n))` имеет не более одного предела, получаем, что если функция `y=f(x)` имеет предел при `x->a`, то этот предел единственный.
На рис. 2 изображена лишь одна последовательность `(x_n)`, которая к тому же является монотонной. Важно понимать, что `lim_(n->oo)f(x_n)=A` для любой последовательности `(x_n)` с условием `x_n!=a` и `lim_(n->oo)x_n=a`.
Доказать, что `lim_(n->oo)x=a`.
Очевидно, функция `f(x)=x` определена на любом интервале, содержащем `a`. Выберем произвольную последовательность `(x_n)` такую, что `x_n!=a` и `lim_(n->oo)x_n=a`. Тогда `f(x_n)=x_n` и, значит, `lim_(n->oo)f(x_n)=a`.
Доказать, что при `a>0lim_(n->a)sqrtx=sqrta`.
Функция `f(x)=sqrtx` определена при `x>=0` и, следовательно, определена на некотором интервале, содержащем `a`. Выберем произвольную последовательность неотрицательных чисел `x_n!=a`, что `lim_(n->oo)x_n=a`. Нам нужно показать, что `lim_(n->oo)sqrtx_n=sqrta`. Фиксируем произвольное `epsilon>0`, тогда найдётся такое число `k`, что при `n>k` выполняется неравенство `|x_n-a| 1)(x^2-1)/(x-1)=2`.
Функция `f(x)=(x^2-1)/(x-1)` определена на любом интервале, содержащем `x=1`, кроме этой точки. Поскольку при `x!=1` имеет место равенство `f(x)=x+1`, то для любой последовательности `(x_n)` такой, что `x_n!=1` и `lim_(n->oo)x_n=1` выполняется `lim_(n->oo)f(x_n)=lim_(n->oo)x_n+1=2`.
Пусть функции `y=f(x)`, `y=g(x)` определены на некотором интервале, содержащем точку `a in R`, за исключением, быть может, самой точки `a`, `lim_(x->a)f(x)=A` и `lim_(x->a)g(x)=B`. Тогда
3) если дополнительно `g(x)!=0` при `x!=a`, `B!=0`, то `lim_(x->a)(f(x))/(g(x))=A/B`.
Эти свойства вытекают из арифметических операций над пределами последовательностей (теорема 2.2). Приведём доказательство для свойства 2. Остальные доказываются аналогично.
Пусть некоторая произвольная последовательность `(x_n)` из интервала, на котором определены функции, такова что `x_n!=a` и `lim_(n->oo)x_n=a`. Тогда по определению предела функции `lim_(n->oo)f(x_n)=A` и `lim_(n->oo)g(x_n)=B`. По пункту 2 теоремы 2.2 `lim_(n->oo)f(x_n)g(x_n)=AB`. По определению предела функции получаем, что `lim_(x->a)f(x)g(x)=AB`.
Пусть функция `y=f(x)` определена на некотором интервале, содержащем точку `a`. Функция `y=f(x)`называется непрерывной в точке `a`, если `lim_(x->a)f(x)=f(a)`, т. е. если для любой последовательности `(x_n)` из области определения функции такой, что `lim_(n->oo)x_n=a`, выполняется равенство `lim_(n->oo)f(x_n)=f(a)`.
Отметим два обстоятельства, связанных с определением непрерывности. Во-первых, оговорка `x_n!=a` здесь не нужна, т. к. при `x_n=a` значения `f(x_n)` равны `f(a)`. Во-вторых, важно понимать, что если функция `y=f(x)` непрерывна в точке `a`, то
1) она определена в точке `a`;
2) существует `lim_(x->a)f(x)=A` и
Если хотя бы один из пунктов 1) – 3) не выполнен, то функция не является непрерывной в точке `a`.
Многочлен является непрерывной на всей числовой прямой функцией.
Из теоремы 3.1 вытекает, что если функции `y=f(x)`, `y=g(x)` непрерывны в точке `a`, то функции `y=f(x)+-g(x)`, `y=f(x)g(x)`, `y=f(x)//g(x)` `(g(a)!=0)` также непрерывны в `a`.
Функция называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.
Функция `y=|x|` непрерывна на всей числовой прямой.
Вообще, все элементарные функции, изучаемые в школьном курсе, непрерывны в каждой точке, в окрестности которой эти функции определены.