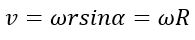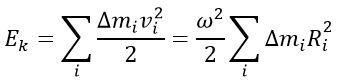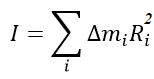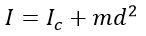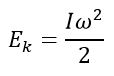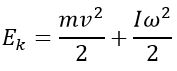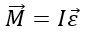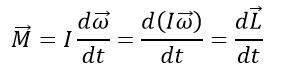как направлен вектор угла поворота чему равен его модуль
Как направлен вектор угла поворота чему равен его модуль
Движение тела как целого можно характеризовать только такими величинами, которые в данный момент времени для всех его точек одинаковы. Поэтому вращательное движение твердого тела характеризуют не линейными, а угловыми величинами: углом поворота Δφ, угловой скоростью ω и угловым ускорением ε.
Угловой скоростью вращения твердого тела называется вектор ω, численно равный первой производной от угла поворота по времени
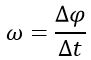
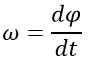
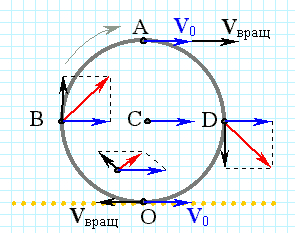
и направленный вдоль оси вращения таким образом, чтобы из его конца вращение было видно происходящим против часовой стрелки. Также направление вектора угловой скорости можно определить по правилу буравчика.
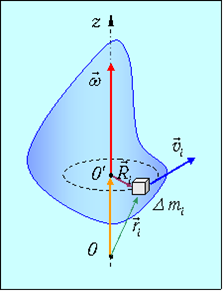
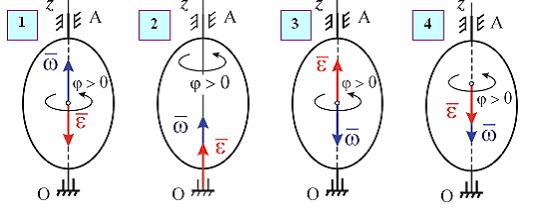
Линейная скорость v произвольной точки М вращающегося тела определяется по формуле Эйлера
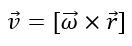
Угловым ускорением вращения твердого тела называется вектор ε, численно равный модулю второй производной от угла поворота по времени или первой производной от угловой скорости по времени
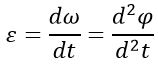
и направленный в ту же сторону, что и вектор угловой скорости, если движение ускоренной и в противоположную сторону от вектора угловой скорости, если движение замедленное. Если тело вращается равномерно, то ε = 0.
Вектор ускорения каждой точки тела, вращающегося вокруг неподвижной оси, можно разбить на две составляющие: нормальное (центростремительное) и тангенциальное. Вектор нормального ускорения направлен к оси вращения, а по модулю определяется по формуле
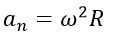
Вектор тангенциального ускорения направлен по касательной к окружности, а по модулю определяется по формуле
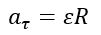
Отсюда модуль полного ускорения определяется по формуле
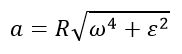
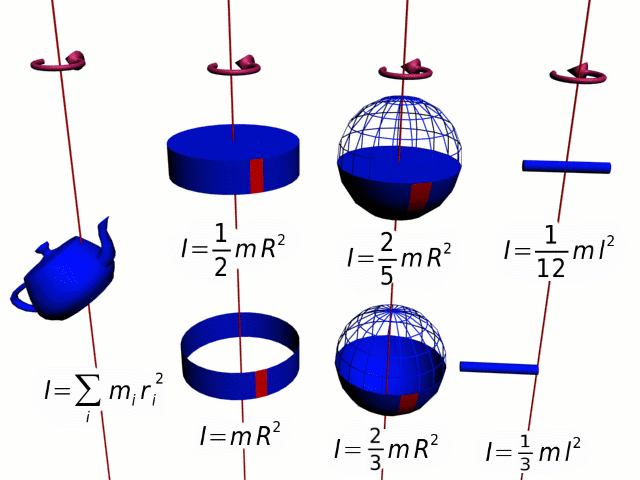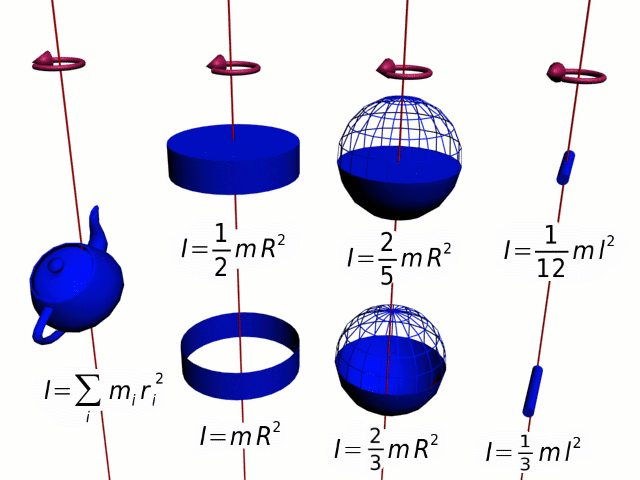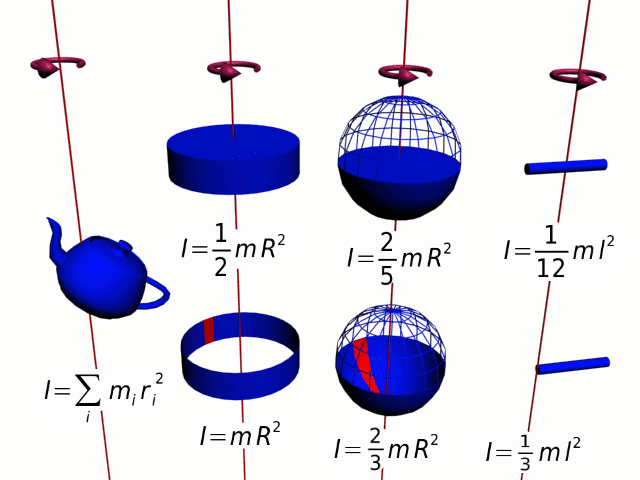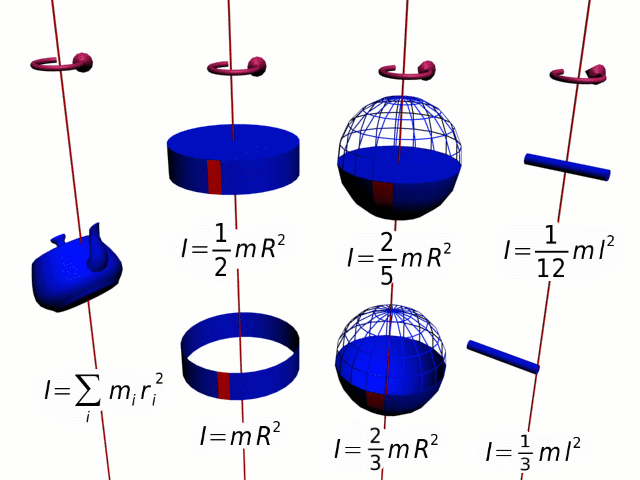
Разобьем вращающееся тело на малые элементы Δmi. Расстояния до оси вращения обозначим через Ri, модули линейных скоростей – через vi. Тогда кинетическую энергию вращающегося тела можно записать в виде:
Физическая величина, зависящая от распределения масс вращающегося тела относительно оси вращения, называется моментом инерции тела относительно данной оси. Это величина, характеризующая инертность тела при вращательном движении.
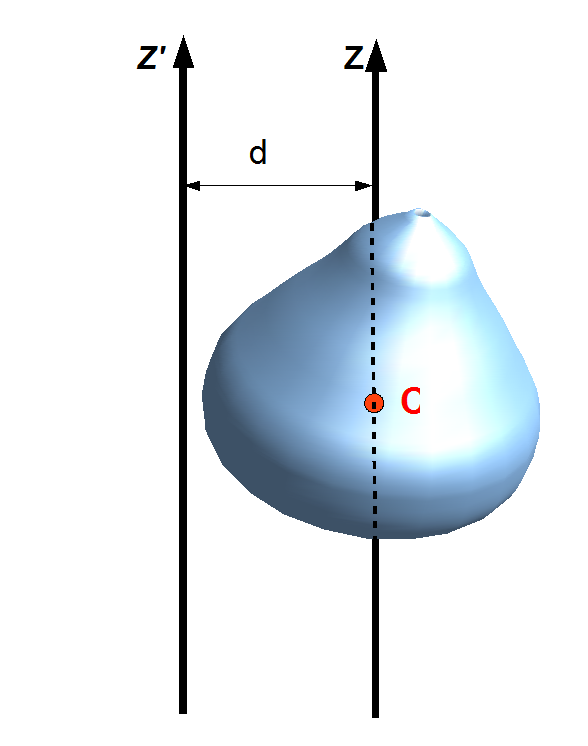
Если твердое тело вращается относительно некоторой неподвижной оси, то его момент инерции I можно выразить через момент инерции I C этого тела относительно оси, проходящей через центр масс тела и параллельной первой. Теорема Штейнера :
Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде
При плоском движении кинетическая энергия движущегося твердого тела равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, проходящей через центр масс тела и перпендикулярной плоскостям, в которых движутся все точки тела :
Для описания вращательного движения вводятся величины, аналогичные тем, которыми характеризуют поступательное движение: момент силы аналогичен силе, момент инерции аналогичен массе.
Основной закон динамики вращательного движения (II закон Ньютона для вращательного движения) имеет вид:
где M – результирующий момент сил, действующий на тело, I – момент инерции тела, ε – угловое ускорение, полученное телом.
Закон сохранения момента импульса:
Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = I ω относительно данной оси сохраняется (момент импульса замкнутой системы остается неизменным):
L = const
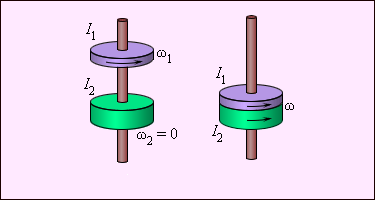
Пример: Неупругое вращательное столкновение двух дисков. Закон сохранения момента импульса: I 1ω1 = ( I 1 + I 2)ω
Аналогия величин и соотношений, характеризующих поступательное и вращательное движения
Магия тензорной алгебры: Часть 6 — Кинематика свободного твердого тела. Природа угловой скорости
Введение
Что такое угловая скорость? Скалярная или векторная величина? На самом деле это не праздный вопрос.
Читая лекции по теоретической механике в университете, я, следуя традиционной методике изложения курса кинематики, вводил понятие угловой скорости в теме «Скорость точки тела при вращательном движении». И там угловая скорость впервые появляется как скалярная величина, со следующим определением.
Угловая скорость твердого тела — это первая производная от угла поворота тела по времени
А вот потом, при рассмотрении каноничной формулы Эйлера для скорости точки тела при вращении
Угловая скорость тела — это псевдовектор, направленный вдоль оси вращения тела в ту сторону, откуда вращение выглядит происходящим против часовой стрелки
Ещё одно частное определение, которое, во-первых, утверждает неподвижность оси вращения, во-вторых навязывает рассмотрение лишь правой системы координат. И наконец термин «псевдовектор» обычно объясняется студентам так: «Посмотрите, ведь мы показали, что омега — скалярная величина. А вектор мы вводим для того, чтобы выписать формулу Эйлера».
При рассмотрении сферического движения оказывается потом, что ось вращения меняет направление, угловое ускорение направлено по касательной к годографу угловой скорости и так далее. Неясности и вводные допущения множатся.
Учитывая уровень подготовки школьников, а так же вопиющую глупость, допускаемую в программах подготовки бакалавров, когда теормех начинается с первого (вдумайтесь!) семестра, такие постепенные вводные, на палках, веревках и желудях наверное оправданы.
Но мы с вами заглянем, что называется, «под капот» проблемы и, вооружившись аппаратом тензорного исчисления, выясним, что угловая скорость — это псевдовектор, порождаемый антисимметричным тензором второго ранга.
Думаю для затравки вполне достаточно, а поэтому — начнем!
1. Свободное движение твердого тела. Тензор поворота
Если движение, совершаемо телом не ограничено связями, то такое его движение называют свободным
Это — самый общий случай движения тела. Следующий рисунок иллюстрирует тот факт, что свободное движение тела можно представить как сумму двух движений: поступательного вместе с полюсом и сферического вокруг полюса.
Рис. 1. Обычная иллюстрация из курса теоретической механики: определение положения свободного твердого тела в пространстве.
Напомню, что речь идет об абсолютно твердом теле, то есть теле, расстояния между точками которого не изменяется с течением времени. Ещё можно сказать, что твердое тело представляет собой неизменяемую механическую систему.
Как видно из рисунка 1, обычной практикой является рассмотрение двух систем координат — одна считается неподвижной и называется базовой, другая
жестко связанна с телом и поворачивается относительно базовой вместе с ним. Такую систему координат называют связанной.
Сначала я тоже хотел ограничиться декартовыми координатами. Но тогда бы мои читатели задали бы мне логичный вопрос — «а зачем тогда тут тензоры?». Поэтому, потратив четыре для в мучительных раздумьях и «нагуляв» окончательное решение пару часов назад, я решил замахнуться на «Вильяма, нашего, Шекспира» и изложить дальнейшие рассуждения в криволинейных координатах.
Рис. 2. Ориентация твердого тела в локальном базисе.
Пусть положение полюса задается вектором
Причем под этим вектором не следует понимать радиус-вектор, так как в криволинейных координатах такое понятие бессмысленно.
В точке O1 задан локальный репер базовой системы координат, образованный тройкой векторов . С движущимся телом связан подвижный репер
. Поворот связанного репера относительно базового можно задать линейным оператором. Получим этот оператор и исследуем его свойства
Рассмотрим некоторую точку M, принадлежащую телу. К ней из полюса можно провести вектор неподвижный относительно связанного репера. Его можно разложить по векторам этого репера
и по векторам базового репера
Каждый вектор связанного репера можно разложить через векторы базового репера
Подставляем (4) в (2) и сравниваем с (3)
Из (5) понятно, что компоненты вектора в базовой системе координат, пересчитываются через его компоненты в связанной системе путем применения линейного оператора
или в безиндексной форме
где столбцы матрицы
– контравариантные компоненты векторов связанного репера по отношению к базовому. Точка, как мы уже отмечали в прошлой статье, обозначает умножение тензоров с последующей сверткой по соседней паре индексов. Линейный оператор
действует на векторы таким образом, что поворачивает их относительно некоторой оси, не меняя длины и угла между векторами. Такое преобразование пространства называется ортогональным. Для того, чтобы таковое преобразование было возможным, оператор (7) должен обладать вполне определенными свойствами. Если длина векторов базиса и углы между ними не меняются, то это означает равенство всех попарных скалярных произведений векторов репера как в базовой, так и в связанной системах координат
Правая часть (8) — это локальный метрический тензор
Преобразование координат при повороте является тождественным для метрического тензора, то есть переводит метрический тензор сам в себя.
В выражении (10) нетрудно увидеть преобразование метрического тензора про смене системы координат, о котором мы подробно говорили в самой первой статье цикла
Стоп! Но мы же знаем, что матрицы поворота обычно ортогональны, то есть произведение матрицы поворота на её транспонированную дает единичную матрицу, иными словами, чтобы обратить матрицу поворота её достаточно транспонировать.
Но ортогональность свойственна матрицам поворота, преобразующим ортонормированный декартов базис. Здесь мы имеем дело с локальным базисом, при повороте которого должны сохранятся длины векторов и углы между ними. Если мы примем базис декартовым, то из (10) мы получим привычные свойства матрицы поворота, к примеру её ортогональность.
Для дальнейших вычислений нам потребуется знать, как будет выглядеть матрица обратного преобразования, то есть . Что же, посмотрим. Для этого умножим (10) слева на
и справа на
откуда незамедлительно получаем
Выходит, что матрица обратного преобразования действительно получается из транспонированной матрицы преобразования, но с участием метрического тензора. Выражения (10) и (11) очень пригодятся нам, а пока сделаем некоторые выводы.
Закон свободного движения твердого тела можно выписать в криволинейных координатах в виде системы уравнений
При этом (12) — закон движения полюса, а (13) — закон сферического движения тела вокруг полюса. При этом (13) — тензор ранга (1,1), называемый тензором поворота.
2. Скорость точки тела при свободном движении. Угловая скорость выходит на сцену
Вычислим скорость точки M, положение которой в связанной системе координат задается постоянными, в силу твердости тела, криволинейными координатами
Из курса теоретической механики известна формула, определяющая скорость точки тела в данном движении
где — скорость полюса;
— скорость точки вокруг полюса.
Так как все координаты, кроме (13) определены относительно базового репера, мы можем записать
Индекс в круглых скобках означает систему координат, в которой берутся компоненты (0 — базовая, 1 — связанная). Дифференцируем (15) по времени с учетом (13)
Перейдем в (16) к связанной системе координат, домножив (15) слева на
где — компонента оператора обратного преобразования
.
Теперь сравним (17) и (14). В последнем слагаемом должно вылезти векторное произведение. Вспоминая определение векторного произведения через тензор Леви-Чивиты, данное во второй статье цикла, замечаем, что на выходе оно дает ковектор, поэтому в (17) перейдем к ковариантым компонентам, домножив это выражение на метрический тензор слева
Теперь представим себе, как выглядел бы ковектор скорости точки относительно плюса, записанный через вектор угловой скорости
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Почему вектор угловой скорости направлен вдоль оси вращения?
| Супермодератор |
Так удобно описывать угловые скорости, это вполне достаточное основание.
| Заслуженный участник |
Viatcheslav1
Это просто людям или в некотором роде лень писать сильно больше, или они боятся, что читателей запутают ещё больше. На самом деле угловая скорость — бивектор, который проще всего представить как ориентированную площадку с площадью, равной модулю угловой скорости, и расположенную в плоскости вращения. Разумеется, если мы введём бивекторы, надо будет объяснять операции с ними и другими величинами и всё такое, так что часто, пользуясь трёхмерностью пространства, вместо них рассматривают их сопряжение Ходжа — просто векторы. Для этого приходится дополнительно задавать ориентацию всего пространства, и когда мы этого не хотим делать, выходят псевдовекторы, про которые вы наверно слышали. На самом деле большинство традиционно псевдовекторных величин, если мы возьмём пространство размерности другой, чем 3, псевдовекторами уже представлять не получится — в двумерии бивектору сопряжён псевдоскаляр, а в четырёхмерии — псевдо-бивектор (и начиная с четырёхмерия нам потому уже придётся разбираться с бивекторами, потому что сопряжение Ходжа ничего не упрощает).
Что же делать с бивекторами и как их грамотно себе представить, чтобы не сделать неправильных выводов — довольно долгая история, можете для начала поискать по форуму.
| Заслуженный участник |
Последний раз редактировалось warlock66613 16.01.2021, 17:51, всего редактировалось 1 раз.
С движением в каком-то направлении связана именно скорость, а не угловая скорость. Почему вектор скорости (обычной, линейной) направлен именно в направлении движения, а не куда-то ещё? Напрамер, не перпендикулярно направлению движения? Очень просто: потому что нас интересует именно направление движения, и мы хотим его закодировать математически. И оказывается, что есть удобный способ это сделать: ввести вектор скорости, который направлен по направлению движения. Если б мы решили характеризовать направление движения перепендикулярным к этому направлению вектором, мы бы не смогли по такому вектору понять как именно движется тело: ведь в трёхмерном пространстве есть много разных направлений, перпендикулярных одному вектору. Поэтому разумный вариант один: характеризовать направление движения с помощью вектора, направленного в этом направлении. А вот если мы рассмотрим движение на плоскости, то там уже можно было бы использовать и такую вот странную «перпендикулярную» скорость вместо обычной.
А теперь рассмотрим вращение в трёхмерном пространстве. Как закодировать математически ориентацию этого вращения? Один из способов — вектор, направленный вдоль оси вращения. Так и получается вектор угловой скорости.
Подитоживая, ответ на ваш вопрос такой: нет причины, почему направление вектора угловой скорости или скорости непременно должно совпадать с направлением какого-либо движения. Всё что требуется от такого вектора — чтобы он однозначно кодировал такое направление или направления. Вектор угловой скорости с этим отлично справляется: зная его можно найти линейную скорость любой точки вращающегося тела.
| Заслуженный участник |
| Заслуженный участник |
Последний раз редактировалось warlock66613 16.01.2021, 20:07, всего редактировалось 1 раз.
Последний раз редактировалось miflin 16.01.2021, 20:42, всего редактировалось 1 раз.
Viatcheslav1
Может рассмотрение частного случая Вам поможет.
Представьте.
Река в северном полушарии течет вдоль меридиана с юга на север.
Какая-то выделенная масса воды обладает линейной скоростью 
направленной вдоль меридиана (эта скорость обеспечивается «уклоном»),
и линейной скоростью 
Cкорость 
и радиусом параллели, на которой находится выделенная масса воды, т.е. 
По мере продвижения этой массы на север неизбежно должна уменьшаться 
т. к уменьшается радиус параллели 
А уменьшение скорости требует силы. Эта сила называется сила Кориолиса.
И вычисление величины и направления силы Кориолиса выражается с помощью формулы,
в которой угловая скорость определена именно как вектор, перпендикулярный плоскости вращения.
| Заслуженный участник |
| Заслуженный участник |
| Заслуженный участник |
Последний раз редактировалось epros 17.01.2021, 15:05, всего редактировалось 4 раз(а).
Если Вас не устраивают простые объяснения, то я могу дать более витиеватое математическое (хм, всё же не настолько витиеватое, как дал arseniiv ). Не знаю, насколько Вы сможете его понять, но будет, по крайней мере, о чём задуматься.