как узнать исходное число по проценту
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор процентов онлайн.
Найти число, зная чему равен указанный процент от него.
Этот калькулятор онлайн решает задачу на нахождение числа, зная его процент.
Онлайн калькулятор для нахождения числа по его процентам не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
Немного теории.
Понятие о проценте
Понятно, что вся рассматриваемая величина составляет 100 сотых, или 100% от самой себя. Поэтому, например, надпись на этикетке «хлопок 100%» означает, что ткань состоит из чистого хлопка, а стопроцентная успеваемость означает, что в классе нет неуспевающих учеников.
Знак «%» получил распространение в конце XVII века. В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «с/о» за дробь и напечатал «%». Так из-за опечатки этот знак вошел в обиход.
Любое число процентов можно записать в виде десятичной дроби, выражающей часть величины.
Чтобы выразить проценты числом, нужно количество процентов разделить на 100. Например:
Для обратного перехода выполняется обратное действие. Таким образом, чтобы выразить число в процентах, надо его умножить на 100:
Задачи на проценты
Поскольку проценты можно выразить дробями, то задачи на проценты являются, по существу, теми же задачами на дроби. В простейших задачах на проценты некоторая величина а принимается за 100% («целое»), а ее часть b выражается числом p%.
В зависимости от того, что неизвестно — а, b или р, выделяются три типа задач на проценты. Эти задачи решаются так же, как и соответствующие задачи на дроби, но перед их решением число р% выражается дробью.
1. Нахождение процента от числа.
Чтобы найти \( \frac
<100>\) от a, надо a умножить на \( \frac
<100>\):
Итак, чтобы найти р% от числа, надо это число умножить на дробь \( \frac
<100>\). Например, 20% от 45 кг равны 45 • 0,2 = 9 кг, а 118% от х равны 1,18x
2. Нахождение числа по его проценту.
Чтобы найти число по его части b, выраженной дробью \( \frac
<100>, \; (p \neq 0) \), надо b разделить на \( \frac
<100>\):
\( a = b : \frac
<100>\)
Таким образом, чтобы найти число по его части, составляющей р% этого числа, надо эту часть разделить на \( \frac
<100>\). Например, если 8% длины отрезка составляют 2,4 см, то длина всего отрезка равна 2,4:0,08 = 240:8 = 30 см.
3. Нахождение процентного отношения двух чисел.
Чтобы найти, сколько процентов число b составляет от а \( (a \neq 0) \), надо сначала узнать, какую часть b составляет от а, а затем эту часть выразить в процентах:
Частное двух чисел, выраженное в процентах, называется процентным отношением этих чисел. Поэтому последнее правило называют правилом нахождения процентного отношения двух чисел.
Нетрудно заметить, что формулы
Составные задачи на проценты решаются аналогично задачам на дроби.
Простой процентный рост
Ясно, что в разных городах и у разных людей квартплата, размер пени и время просрочки разные. Поэтому имеет смысл составить общую формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.
Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.
Аналогичная формула получится, если некоторая величина уменьшается за данный период времени на определенное число процентов. Как и выше, нетрудно убедиться, что в этом случае
\( S_n = \left( 1- \frac
Эта формула также называется формулой простого процентного роста, хотя заданная величина в действительности убывает. Рост в этом случае «отрицательный».
Сложный процентный рост
Если же вкладчик этого не сделал, то проценты присоединяются к начальному вкладу (капитализируются), и поэтому в конце следующего года 10% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.
Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк 1000 р. и ни разу в течение трех лет не будет брать деньги со счета.
10% от 1000 р. составляют 0,1 • 1000 = 100 р., следовательно, через год на его счете будет
1000 + 100 = 1100 (р.)
10% от новой суммы 1100 р. составляют 0,1 • 1100 = 110 р., следовательно, через 2 года на его счете будет
1100 + 110 = 1210 (р.)
10% от новой суммы 1210 р. составляют 0,1 • 1210 = 121 р., следовательно, через 3 года на его счете будет
1210 + 121 = 1331 (р.)
Нетрудно представить себе, сколько при таком непосредственном, «лобовом» подсчете понадобилось бы времени для нахождения суммы вклада через 20 лет. Между тем подсчет можно вести значительно проще.
А именно, через год начальная сумма увеличится на 10%, то есть составит 110% от начальной, или, другими словами, увеличится в 1,1 раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 10%. Следовательно, через 2 года начальная сумма увеличится в 1,1 • 1,1 = 1,1 2 раз.
Решим теперь эту задачу в общем виде. Пусть банк начисляет доход в размере р% годовых, внесенная сумма равна S р., а сумма, которая будет на счете через n лет, равна Sn р.
Величина p% от S составляет \( \frac
<100>S \) р., и через год на счете окажется сумма
\( S_1 = S+ \frac
<100>S = \left( 1+ \frac
<100>\right)S \)
то есть начальная сумма увеличится в \( 1+ \frac
<100>\) раз.
За следующий год сумма S1 увеличится во столько же раз, и поэтому через два года на счете будет сумма
\( S_2 = \left( 1+ \frac
<100>\right)S_1 = \left( 1+ \frac
<100>\right) \left( 1+ \frac
<100>\right)S = \left( 1+ \frac
<100>\right)^2 S \)
Аналогично \( S_3 = \left( 1+ \frac
<100>\right)^3 S \) и т.д. Другими словами, справедливо равенство
\( S_n = \left( 1+ \frac
<100>\right)^n S \)
Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.
Формула простого процента: как найти исходное значение
В этом коротком видеоуроке мы научимся решать задачи на проценты с помощью специальной формулы, которая так и называется: формула простого процента. Давайте оформим эту формулу в виде теоремы.
Плюс или минус перед коэффициентом k ставится в зависимости от условия задачи. Если по условию величина x возрастает, то перед k стоит плюс. Если же величина уменьшается, то перед коэффициентом k стоит минус.
Несмотря на кажущуюся мудреность этой формулы, многие задачи с ее помощью решаются очень быстро и красиво. Давайте попробуем.
Задача. Цена на товар была повышена на 10% и составила 2970 рублей. Сколько рублей стоил товар до повышения цены?
Складываем числа в числителе и получаем:
Сокращаем по одному нулю в числителе и знаменателе, а затем умножаем обе части уравнения на 10. Получим:
Чтобы найти x из этого простейшего линейного уравнения, нужно разделить обе стороны на 11:
x = 29 700 : 11 = 2700
Как видите, это довольно большие числа, поэтому в уме такие вычисления не провести. В случае, если такая задача встретится вам на ЕГЭ, придется делить уголком. При этом все разделилось без остатка, и мы получили значение x :
Именно столько стоил товар до повышения цены. И именно это число нам требовалось найти по условию задачи. Поэтому все: задача решена. Причем решена не «напролом», а с помощью формулы простого процента — быстро, красиво и наглядно.
Разумеется, эту задачу можно было решать по-другому. Например, через пропорции. Или экзотическим методом коэффициентов. Но будет гораздо лучше и надежнее, если у вас на вооружении будет несколько приемов для решения любой задачи на проценты. Так что обязательно попрактикуйтесь в использовании данной формулы.
А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)
Калькулятор процентов
Используя калькулятор процентов Вы сможете производить всевозможные расчеты с использованием процентов. Округляет результаты до нужного количества знаков после запятой
Сколько процентов составляет число X от числа Y. Какое число соответствует X процентам от числа Y. Прибавление или вычитание процентов из числа.
Калькулятор разработан специально для расчета процентов. Позволяет выполнять разнообразные расчеты при работе с процентами. Функционально состоит из 4-х разных калькуляторов. Примеры вычислений на калькуляторе процентов смотрите ниже.
| ||
| Сколько составляет % от числа | ||
| 0% от числа 0 = 0 | ||
| Сколько % составляет число от числа | ||
| Число 0 от числа 0 = 0% | ||
| Прибавить % к числу | ||
| Прибавить 0% к числу 0 = 0 | ||
| Вычесть % из числа | ||
| Вычесть 0% из числа 0 = 0 | ||
|
Примеры вычислений на калькуляторе процентов
Калькулятор процентов онлайн
Калькулятор процентов разработан для различных вычислений с процентами. Функционал состоит из 11 независимых калькуляторов. Есть возможность настроить количество значимых чисел. Примеры работы с калькулятором смотрите ниже.
Процент от числа
Чтобы вычислить процент от числа необходимо число умножить на процент и разделить на 100%
Формула нахождения процента от числа
Прибавить процент к числу
Чтобы прибавить процент к числу нужно сначала найти процент от этого числа. Затем прибавить полученное значение к исходному числу
Формула прибавления процента к числу
Разделить число на процент
Для деления числа на процент от этого числа нужно найти процент от этого числа, затем число разделить на полученное число.
Формула деления числа на процент от этого числа
Умножить число на процент
Для умножения числа на процент от этого числа нужно найти процент от этого числа а затем умножить на число.
Формула умножения числа на процент от этого числа
Вычислить сколько процентов составляет число от числа
Чтобы вычислить сколько процентов составляет число от другого числа, нужно первое число умножить на 100% и разделить на второе число.
Формула вычисления процента числа от другого числа
Проценты в десятичную дробь
Чтобы представить проценты в виде десятичной дроби нужно проценты разделить на 100%
Проценты в обыкновенную дробь
Чтобы представить проценты в виде обыкновенной дроби нужно проценты представить в виде десятичной дроби. Затем десятичную дробь преобразовать в обыкновенную дробь.
1) Считает процент от числа.
2) Считает сколько процентов составляет одно число от другого.
3) Прибавлять процент к числу.
4) Отнимает процент от числа.
5) Вычисляет число по проценту от него.
6) Считает на сколько процентов первое число меньше второго.
7) Считает на сколько процентов первое число больше второго.
8) Умножает число на процент от этого числа.
9) Делит число на процент от этого числа.
10) Переводит процент в десятичную дробь.
11) Переводит процент в обыкновенную дробь.
Пример 1. Сколько составляет 20% от числа 160
Пример 2. Сколько % составляет число 50 от числа 200
Пример 3. Прибавить 20% к числу 250
250 / 100% * 20% + 250 = 300
Пример 4. Вычесть 20% из числа 250
Пример 5. Вычислить число если 20% от него равно 55
Пример 6. На сколько процентов число 50 меньше числа 100
Пример 7. На сколько процентов число 100 больше числа 50
Пример 8. Умножить число 20 на 25 процентов от этого числа
20 * 20 * 25% /100% = 100
Пример 9. Разделить число 80 на 25 процентов от этого числа
80 / ((80 × 25%) / 100%) = 4
Пример 10. Преобразовать 25% в десятичную дробь
Пример 11. Преобразовать 20% в обыкновенную дробь
Проценты.
Проценты мы видим достаточно часто в повседневной жизни. Возьмем плитку шоколада, пачку мороженого на которых написано «56 % какао», «пломбир 100 % ». А что такое процент?
Процентом называется одна сотая часть. Кратко записывают 1 %. Знак % заменяет слово «процент».
Какое бы число или величину мы не взяли, его сотая часть — это один процент данного числа или величины. Например, для числа 400 (0,01 числа 400) — это число 4, поэтому 4 — это 1 % числа 400; 1 гривны (0,01 гривны) — это 1 копейка, поэтому 1 копейка — это 1 % гривны.
Пазл содержит 500 элементов. Сколько элементов приходится на 1 его процент? Пусть 500 элементов пазла — это 100 %. Тогда на 1 % приходится в 100 раз меньше его элементов. Отсюда 500 : 100 = 5 (эл.). Итак, 1 % — это 5 элементов пазла.
Марине надо пришить тесьму, 3 см которой составляет 1 % от её длины. Марина пришила 50 % тесьмы, Сколько сантиметров тесьмы она пришила? Поскольку 50 % больше 1 % в 50 раз, то Марина пришила тесьмы в 50 раз больше, чем 3 см. Отсюда 3•50 = 150 (см). Итак, Марина пришила 150 см тесьмы.
Груши сладких сортов содержат 15 % сахара. Сколько сахара содержится в 3 кг груш?
Составим краткую запись данных задачи.
1. Сколько килограммов соответствует 1 %?
2. Сколько килограммов приходится на 15 %?
И так, в 3 кг груш содержится 0,45 кг сахара.
Чтобы найти процент от числа, нужно данное число разделить на 100 и результат умножить на количество процентов.
В украинском веночке Марины 20 % всех лент голубые. Сколько всего лент в веночке, если голубых — 5?
Составим краткую запись данных задачи.
Голубые ленты: 5 — 20%
Итак, в веночке Марины 25 лент.
Чтобы найти число по его проценту, нужно данное число разделить на количество процентов и результат умножить на 100.
Достаточно часто необходимо найти процентное выражение одного числа от другого.
Завод произвел за 2014 год 40000 деталей, а в следующем году – только 36000 штук. Сколько процентов это составило по отношению к выпуску предыдущего года?
Составим краткую запись:
Итак, в 2015 выпуск составил 90 % от 2014 года
Правило нахождения процентного выражения числа от другого.
Чтобы найти процентное выражение числа от другого, нужно данное число разделить на первое и результат умножить на 100.
Процентное отношение двух чисел — это их отношение, выраженное в процентах. Процентное отношение показывает, сколько процентов одно число составляет от другого.
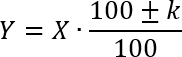
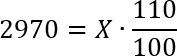
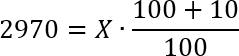
 Добавить в Избранное
Добавить в Избранное