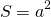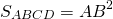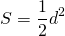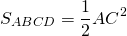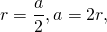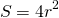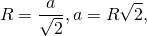как узнать площадь квадрата

Как определить площадь квадрата

Формула нахождения площади квадрата

Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.

Если известна длина стороны

Умножаем ее на то же число или возводим в квадрат.

Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.

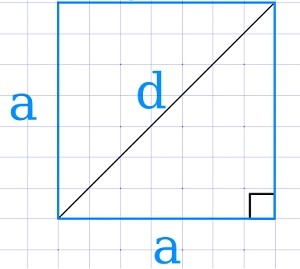
Если нам дана диагональ

Возводим ее в квадрат и делим на два.

S = d 2 : 2, где d — диагональ.

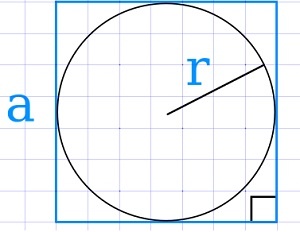
Если известен радиус вписанной окружности

Умножаем его квадрат на четыре.

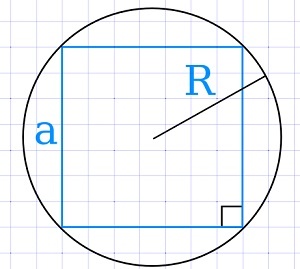
Если у нас есть радиус описанной окружности

Возведем его в квадрат и умножим на два.

У нас есть дополнительные занятия по математике для учеников с 1 по 11 классы — записывайтесь!

Если есть периметр

Мы должны возвести его в квадрат и разделить на 16.

S = Р 2 : 16, где Р — это периметр.

Периметр любого четырехугольника равен сумме длин всех его сторон.

Популярные единицы измерения площади:

S квадрата. Решение задач

Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!

Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.

Воспользуемся формулой: S = d 2 : 2.

Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.

Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d

Диаметр окружности равен двум радиусам:
d = 2r

Получается, что сторона равна двум радиусам:
a = 2r

Используем формулу нахождения площади квадрата через сторону:
S = a 2

Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r) 2
S = 4r 2

Теперь подставим значение радиуса в формулу площади:
S = 4 × 24 2 = 2304 см 2

Источник

площадь квадрата

Площадь квадрата, как посчитать площадь квадрата. Формула площади квадрата.

О квадрате и его площади

Формула площади квадрата.

Сторона квадрата обозначается любой буквой, которая вам нравится, кроме занятой S.

Формула площади квадрата : площадь квадрата равна стороне квадрата во второй степени.

Либо может встречаться вот такая формулировка площади квадрата:

Площадь квадрата равна произведению стороны квадрата на себя.

Пример подсчета площади квадрата

Как вычислить площадь квадрата?

Предположим, что у нас есть квадрат, площадь которого нам требуется узнать!

Пусть это будет 10см.

Сколько будет площадь квадрата со стороной 10см.

Умножаем сторону квадрата 10, на себя, на 10 :

10 * 10 = 100см 2 Ответ :

Площадь квадрата со стороной 10см, будет равна 100см 2 100см 2

Как найти площадь квадрата если известен периметр!?

Условие задачи : найдите площадь квадрата, если известен периметр = 32см.

Для того, чтобы узнать площадь квадрата по его периметру нам понадобится формула подсчета периметра квадрата:

Далее нам нужно 32 разделить на 4, мы найдем длину одной стороны квадрата.

И далее по формуле площади квадрата узнаем его площадь :

Квадрат, у которого периметр 32 см, площадь равна 16см²

Как найти площадь квадрата если известна диагональ!?

Условие задачи : найдите площадь квадрата, если известна диагональ квадрата = 8см.

Для того, чтобы найти диагональ квадрата, нам нужно вспомнить формулу пифагора :

Немного нужно преобразовать :

А если S = a², то S = d²/2

И далее нам нужно подставить нашу диагональ :

Какая единица измерения площади квадрата!?

После того, как я написал страницу и началась выдача страницы, интересный поисковый вопрос : «площадь квадрата почему см2«.

Человек, видимо, хотел спросить, откуда двойка в единице измерения площади квадрата!?

Мы можем рассказать. о том, в какой единице измерения измеряются площадь квадрата и откуда там берется двойка!?

Единица измерения площади квадрата

Почему единица измерения площади квадрата пишется с двойкой

Обычно в младших классах, на единицу измерения не обращают внимания. Но уже в старших классах на это обращают некоторое внимание!

Почему единица площади(и в том числе квадрата) обозначают двойкой чуть выше буквеного выражения!?

Если мы вспомним, что площадь квадрата равна умноженной длины стороны на себя и напишем единицу измерения. то мы увидим откуда берется двойка.

Давайте покажем на примере.

Пусть надо найти площадь квадрата со стороной 12 см.

Так и записываем в формулу :

Далее никуда единицу измерения не убираем, а умножаем их между собой, вот отсюда и получается квадратные сантиметры(или другая мера длины в квадрате) :

12*12(см*см) = 12²см² = 144см²

Как найти площадь квадрата зная радиус вписанной окружности!?

Как найти площадь квадрата зная радиус вписанной окружности!?

Это очень простая задача!

Диаметр вписанной окружности равна стороне квадрата.

Диаметр окружности равен 2R.

Значит сторона квадрата равна 2R.

Значит площадь квадрата равна S = (2R)²

Как найти площадь квадрата зная радиус описанной окружности!?

Как найти площадь квадрата зная радиус описанной окружности!?

Данная задача такая же простая, как и выше описанная!

У нас известен радиус окружности описанной вокруг квадрата.

Диаметр окружности AB равен диагонали квадрата AB и мы знаем, что диаметр окружности равен двум радиусам d = 2R.

Далее подставляем S = (2R)²/2

Найти площадь квадрата онлайн

Для того чтобы посчитать площадь квадрата онлайн, вам требуется в поле :

Источник

Как найти площадь фигуры

Обозначение площади

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Если параметры фигуры переданы в разных единицах измерения длины, мы не сможем решить ни одну задачу. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

Круг — это множество точек на плоскости, ограниченных окружностью, удаленных от центра на равном радиусу расстоянии. Радиусом принято называть отрезок, соединяющий центр с любой точкой окружности.

S = &pi × d 2 : 4;, где d — это диаметр.

S = L 2 ​ : (4 × π), где L — это длина окружности.

Треугольник

Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, соединенных тремя отрезками. Эти три точки принято называть вершинами, а отрезки — сторонами. Рассчитать площадь треугольника можно несколькими способами по исходными данным, давайте их рассмотрим.

1. Если известна сторона и высота.

S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:

2. Если известны две стороны и синус угла.

S = 0,5 × a × b * sinα, где a и b — две стороны, sinα — синус угла между ними.

3. Если есть радиус описанной окружности.

S = (a × b × с) : (4 × R), где a, b и с — стороны треугольника, а R — радиус описанной окружности.

4. Если есть радиус вписанной окружности.

S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

У нас есть отличные онлайн-занятия с лучшими преподавателями по математике для учеников с 1 по 11 классы!

Прямоугольник

Прямоугольник — четырехугольник, у которого все стороны пересекаются под прямым углом. Узнать площадь прямоугольника помогут следующие формулы:

S = a × b, где a, b — длина и ширина прямоугольника.

Диагональ — это отрезок, который соединяет несмежные вершины многоугольника. Она есть во всех фигурах, число вершин которых больше трех.

S = 0,5 × d 2 × 𝑠𝑖𝑛(𝑎), где d — диагональ, α — угол между диагоналями.

Квадрат

Квадрат — это тот же прямоугольник, но при условии, что все его стороны равны. Найти его площадь легко:

S = d 2 : 2, где d — диагональ.

Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны и две не параллельны.

S = 0,5 × (a + b) × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны под прямым углом.

Параллелограмм и ромб

Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны.

Ромб — это параллелограмм, у которого все стороны равны.

Расскажем про общие формулы расчета площади параллелограмма и ромба.

S = a × h, где a — сторона, h — высота.

S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a 2 × sinα.

Для ромба: S = 0,5 × (d₁ × d₂), где d₁, d₂ — две диагонали. Для параллелограмма: S = 0,5 × (d₁ × d₂) × sinβ, где β — угол между диагоналями.

Источник

Как найти площадь квадрата

Как найти площадь квадрата?

Площадь квадрата может быть найдена по его стороне, диагонали, радиусам вписанной и описанной окружности.

1. Площадь квадрата равна квадрату его стороны.

Формула для нахождения площади квадрата по его стороне:

Например, площадь квадрата ABCD можно найти как квадрат его стороны AB:

2. Площадь квадрата равна половине квадрата диагонали его стороны.

Формула для нахождения площади квадрата по его диагонали:

Например, площадь квадрата ABCD можно найти через его диагональ AC:

3. Площадь квадрата в четыре раза больше квадрата радиуса вписанной к него окружности.

Так как

то из формулы площади квадрата по стороне получаем

формулу для нахождения площади квадрата через радиус вписанной окружности:

4. Площадь квадрата равна удвоенному квадрату радиуса описанной около него окружности.

Так как

то из формулы площади квадрата по стороне вытекает

формула для нахождения площади квадрата через радиус вписанной окружности:

Источник

Как вычислить площадь квадрата

Квадрат

Квадрат — геометрическая фигура, являющаяся правильным четырехугольником. В правильном четырехугольнике все стороны и углы равны.

Нахождение площади квадрата

Через длину стороны

По аналогии с площадью прямоугольника можно вывести формулу:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

где а — сторона квадрата.

Через диагональ

где d — диагональ квадрата.

Также, стоит отметить, что в квадрате соотношение стороны и диагонали:

Через радиус вписанной окружности

где r — радиус вписанной окружности.

Через радиус описанной окружности

где R — радиус описанной окружности.

Через периметр

где Р — периметр квадрата.

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

© 2021 fenix.help Все права защищены

Подпишитесь на полезные материалы для студента!

и получи в подарок:

Источник