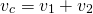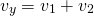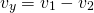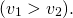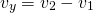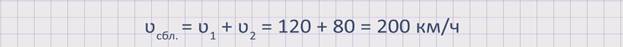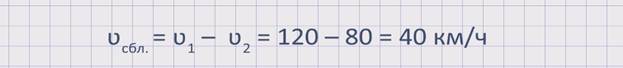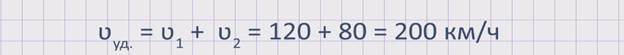как узнать скорость удаления
Скорость сближения и скорость удаления
Как найти скорость сближения и скорость удаления? Ответ зависит от вида движения.
Чтобы найти скорость сближения, надо сложить скорости объектов:
Чтобы найти скорость удаления, надо сложить скорости объектов:
III. При движении в одном направлении объекты могут как сближаться, так и удаляться.
Если объекты вышли одновременно из одного пункта с разными скоростями, то они удаляются.
Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
Если объекты выходят одновременно из разных пунктов и движутся в одном направлении, то это — движение вдогонку.
Если скорость идущего впереди объекта меньше скорости объекта, следующего за ним, то они сближаются.
Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:
Если объект, идущий впереди, движется с большей скоростью, чем идущий следом за ним, то они удаляются:
Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
Если из одного пункта в одном направлении выходит сначала один объект, а спустя некоторое время вслед за ним — другой, то рассуждаем аналогично: если скорость идущего впереди больше, то объекты удаляются, если скорость идущего впереди меньше — сближаются.
При движении навстречу друг другу и движении в противоположных направлениях скорости складываем.
При движении в одном направлении скорости вычитаем.
Задачи на движение в одном направлении
Рассмотрим задачи, в которых речь идёт о движении в одном направлении. В таких задачах два каких-нибудь объекта движутся в одном направлении с разной скоростью, отдаляясь друг от друга или сближаясь друг с другом.
Задачи на скорость сближения
Скорость сближения — это скорость, с которой объекты сближаются друг с другом.
Чтобы найти скорость сближения двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача 1. Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?
Решение: Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на:
Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:
Решение задачи по действиям можно записать так:
1) 40 · 4 = 160 (км) — расстояние между автомобилями,
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 2. Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:
Решение задачи по действиям можно записать так:
Ответ: Через 5 часов второй пешеход догонит первого.
Задача на скорость удаления
Скорость удаления — это скорость, с которой объекты отдаляются друг от друга.
Чтобы найти скорость удаления двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача. Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго — 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение: Сначала узнаем скорость удаления автомобилей друг от друга, для этого вычтем из большей скорости меньшую:
Каждый час автомобили отдаляются друг от друга на 40 км. Теперь можно узнать сколько километров будет между ними через 3 часа, для этого скорость удаления умножим на 3:
Чтобы узнать через сколько часов расстояние между автомобилями станет 200 км, надо расстояние разделить на скорость удаления:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Как узнать скорость удаления
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке познакомимся с такими понятиями, как «скорость сближения» и «скорость удаления».
Для ознакомления с понятиями «скорость сближения» и «скорость удаления» рассмотрим 4 реальные ситуации.
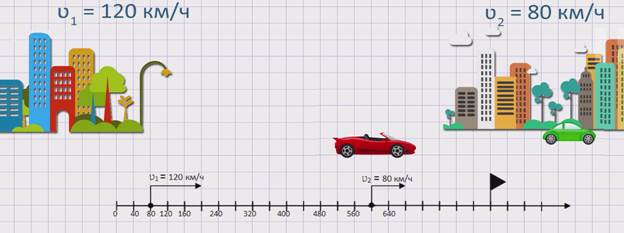
Из двух городов навстречу друг другу одновременно выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Сокращается ли расстояние между автомобилями? Если да, то с какой скоростью?
Изобразим движение данных автомобилей на координатном луче.
Из рисунка видно, что два автомобиля, двигаясь навстречу друг другу, приближаются. Значит, расстояние между ними сокращается. Чтобы узнать, с какой скоростью сокращается расстояние между автомобилями или же с какой скоростью сближаются два автомобиля, необходимо к скорости первого автомобиля прибавить скорость второго. А именно, скорость сближения равна сумме скоростей первого и второго автомобилей: ʋсбл. = ʋ1 +ʋ2.
Найдем скорость сближения данных автомобилей:
Значит, расстояние между автомобилями сокращается со скоростью 200 км/ч. Рассмотрим вторую ситуацию.
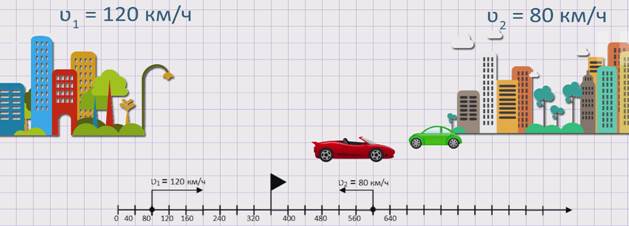
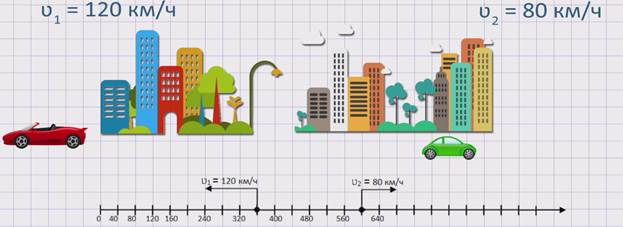
Из двух городов одновременно в одном направлении, вдогонку, выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Сокращается или увеличивается расстояние между автомобилями и на сколько?
Изобразим движение данных автомобилей на координатном луче.
Рассматривая приведенные выше ситуации, мы познакомились с понятием «скорость сближения». Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.
Рассмотрим следующую третью ситуацию.
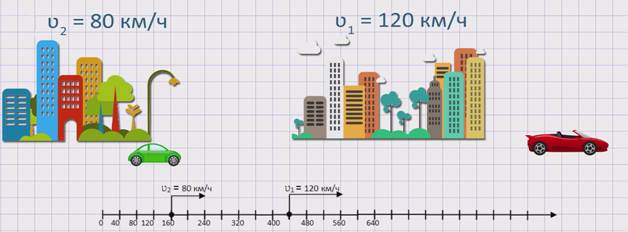
Из двух городов в противоположных направлениях одновременно выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Будет ли увеличиваться расстояние между автомобилями? Если да, то на сколько?
Изобразим движение данных автомобилей на координатном луче.
Найдем скорость удаления данных автомобилей: ʋуд. = ʋ1 + ʋ2 = 120 + 80 = 200 км/ч. Значит, расстояние между автомобилями увеличивается со скоростью 200 км/ч.
Рассмотрим последнюю четвертую ситуацию.
Из двух городов водном направление одновременно выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Причем второй автомобиль движется с отставанием. Будет увеличиваться или уменьшаться расстояние между автомобилями и на сколько?
Изобразим движение данных автомобилей на координатном луче.
Рассматривая приведенные выше ситуации, мы познакомились с понятием «скорость удаления». Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени.
1.Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.
2.При движении двух объектов навстречу друг другу скорость сближения равна сумме скоростей этих объектов. ʋсбл. = ʋ1 + ʋ2
4.Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени.
5.При движении двух объектов в противоположных направлениях скорость удаления равна сумме скоростей этих объектов. ʋуд. = ʋ1 + ʋ2
Математика. 5 класс
Конспект урока
Задачи на движение
Перечень вопросов, рассматриваемых в теме:
Расстояние – это длина от одного пункта до другого.
Большие расстояния, в основном, измеряются в метрах и километрах.
Расстояние обозначается латинской буквой S.
Чтобы найти расстояние, надо скорость умножить на время движения:
Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Скорость обозначается латинской буквой v.
Чтобы найти скорость, нужно расстояние разделить на время движения:
Время – это продолжительность каких-то действий, событий.
Время движения обозначается маленькой латинской буквой t.
Чтобы найти время, нужно расстояние разделить на скорость движения:
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010
1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014
2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.
3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010
Теоретический материал для самостоятельного изучения
Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.
Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.
Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?
Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.
Давайте найдём скорость первого школьника. Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:
Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:
Скорость движения первого школьника составляет 4 метра в секунду.
Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:
200 м : 100 c = 2 (м/с)
Скорость движения первого школьника – 4 (м/с).
Скорость движения второго школьника – 2 (м/с).
Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.
Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние. Время движения обозначается маленькой латинской буквой t.
От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?
Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:
Ответ: мы доедем до спортивной секции за 2 минуты.
Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
Мы вышли из дома и направились в магазин. Мы дошли до магазина за 15 минут. Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?
Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:
S = v ∙ t = 60 ∙ 15 = 900 (метров)
Ответ: мы прошли 900 метров.
Если известно время и расстояние, то можно найти скорость:
Расстояние от дома до школы 800 метров. Школьник дошёл до этой школы за 8 минут. Какова была его скорость?
Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:
v = S : t = 800 : 8 = 100 (м/мин)
Ответ: скорость школьника была 100 м/мин.
Если известна скорость и расстояние, то можно найти время:
От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?
Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?
Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:
t = S : v = 600 : 120 = 5 (минут).
Ответ: мы дойдём до спортивной секции за 5 минут.
Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:
Теперь рассмотрим типы задач на движение.
Задачи на сближение.
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
13 км/ч + 15 км/ч = 28 км/ч
Ответ: расстояние между населёнными пунктами 84 км.
Задачи на скорость удаления.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?
Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.
Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.
Задачи на движение объектов в одном направлении.
В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?
130 км/ч − 90 км/ч = 40 км/ч
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.
Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.
Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):
Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.
В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:
900 + 85 – 90 = 985 – 90 = 895 м
Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров. Это был наш ответ на первый вопрос задачи:
900 + 255 – 270 = 1155 – 270 = 885 м
Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.
А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:
Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Скорость сближения и скорость удаления
Презентация к уроку
Воспитательные: воспитание интереса к математике;
– Здравствуйте, ребята, садитесь! Проверьте, все ли у вас готово к уроку.
– Вспомним правила посадки.
– Запишите число.
Цель урока (Постановка учебной задачи).
– Вспомните, пожалуйста, сколько объектов может одновременно двигаться по числовому лучу? Откуда могут начинать свое движение объекты? В каких направлениях могут двигаться объекты? С какой скоростью могут двигаться объекты?
– Сегодня мы выясним, что такое “скорость сближения”, “скорость удаления”, что нужно знать, чтобы определить, какая это скорость, как найти скорость сближения или удаления.
– Запишем тему урока “Скорость сближения и скорость удаления”.
Выполняются на доске 2-мя учащимися во время математического диктанта.
| S | V | t | Формула |
| I | ? км | 45 км/ч | 7 ч |
| II | 180 м | ? м/мин | 5 мин |
| III | 960 м | 16 м/с | ? с |
| IV | ? км | 60 км/ч | 60 мин |
Изобразите движение точек на координатном луче и запишите формулу движения точек:
Проверка математического диктанта и индивидуальных заданий.
Проверка математического диктанта.
– В ответах математического диктанта зашифровано слово. Чтобы расшифровать его, нам поможет алфавит русского языка.
– Каждый ответ соответствует порядковому номеру буквы в алфавите. Выпишите буквы в строчку.
Переход на Слайд 2 “Математический диктант”.
– Что у вас получилось? Проверяем.
По каждому клику на Слайде 2 заполняется один столбец таблицы.
– У кого получилось слово “скорость”, ставит себе 5.
– На какие 2 группы можно разделить числа математического диктанта?
– Что такое “скорость движения”?
Проверка задания 1.
| S | V | t | Формула | |
| I | 315 км | 45 км/ч | 7 ч | S=V*t |
| II | 180 м | 36 м/мин | 5 мин | V=S:t |
| III | 960 м | 16 м/с | 6 с | t=S:V |
| IV | 60 км | 60 км/ч | 60 мин | S=V*t |
– Как найти расстояние, зная скорость и время объекта?
– Как найти скорость, зная расстояние и время объекта?
– Как найти время, зная расстояние и скорость объекта?
Проверка задания 2.
– Сравните 2 чертежа. Что заметили? В чем отличие? Одинаковы ли виды скоростей?
– Как вы думаете, на каком чертеже будет идти речь о скорости сближения, а где – о скорости удаления?
Физкультминутка для глаз.
Объяснение понятий “скорость сближения” и “скорость удаления”.
Работа с упражнением 1 урока 24 (Слайды 3–6). По ходу объяснения ученикам задаются вопросы о том, что они видят на экране и после их ответов ученик заполняет таблицу на доске, остальные — в учебниках, затем учитель переходит к следующему шагу анимации.
Переход на Слайд 3 “1) Встречное движение”.
– Посмотрите на экран.
– Что вы можете сказать о движении Мальвины и Буратино?
– Какое это движение?
– Из каких точек началось их движение? Заполним таблицу.
– В какой точке оказались Мальвина и Буратино через 1 минуту, через 2 минуты, через 3 минуты? Заполним таблицу.
– Что происходит с расстоянием между объектами?
– На сколько уменьшается расстояние между ними через каждую минуту?
– В какой точке и через сколько минут произошла встреча?
– Сделаем вывод.
Переход на Слайд 4 “2) Движение в противоположных направлениях”.
– Посмотрите на экран.
– Что вы можете сказать о движении Синьора Помидора и Чиполлино?
– Какое это движение? Заполним таблицу.
– Из каких точек началось их движение? Заполним таблицу.
– В какой точке оказались Синьор Помидор и Чиполлино через 1 минуту, через 2 минуты, через 3 минуты? Заполним таблицу.
– Что происходит с расстоянием между объектами?
– На сколько увеличивается расстояние между ними через каждую минуту?
– Произойдет ли встреча?
– Сделаем вывод.
Переход на Слайд 5 “3) Движение вдогонку”.
Переход на Слайд 6 “4) Движение с отставанием””.
– Посмотрите на экран
– Что вы можете сказать о движении Пончика и Незнайки?
– Какое это движение?
– Из каких точек началось их движение?
– В какой точке оказались Пончик и Незнайка через 1 минуту, через 2 минуты, через 3 минуты? Заполним таблицу.
– Что происходит с расстоянием между объектами? Почему?
– На сколько увеличивается расстояние между ними через каждую минуту?
– Произойдет ли встреча?
– Сделаем вывод.
– Что такое “скорость сближения”? (Это расстояние, на которое сближаются объекты за единицу времени.)
– Что такое “скорость удаления”? (Это расстояние, на которое удаляются объекты за единицу времени.)
Составление опорной схемы.
Переход на Слайд 7 “Опорная схема”.
– Составим опорные схемы ко всем видам движения.
Мы к лесной лужайке вышли,
Поднимая ноги выше,
Через кустики и кочки,
Через ветви и пенечки.
Кто высоко так шагал –
Не споткнулся, не упал.
Решение задач с комментированием.
Для закрепления знаний учащимися разбираются и решаются задачи на все виды движения.
– Решим несколько задач и определим, о какой скорости: сближения или удаления идет речь? Чему она равна? А помогут нам в этом герои сказки “Золотой ключик”.
Работа со Слайдами 8–11. Ученики определяют по Слайду, к какой опорной схеме относится задача, и предлагают способ ее решения.
Самостоятельное решение задач (тест).
Для проверки знаний и умений по данной теме учащиеся получили тестовые карточки с заданием “Установите соответствие между схемой задачи и ее решением (1 и 2 варианты)”.
– Рассмотрите схемы задач, определите, о какой скорости движения идет речь (сближения или удаления), соедините с подходящим выражением и вычислите его.
Взаимопроверка решений задач.
Учащиеся проверяют выполнение задания с помощью Слайдов 12–13.
– Подошёл к концу наш урок. О чем сегодня узнали на уроке? Что важно знать, чтобы определить скорость сближения или удаления? Что вам особенно понравилось, запомнилось?
Выставление отметок и поощрение учеников.
В течение всего урока работа и ответы учеников оценивались словесно и поощрительными медальками.
Список использованных источников и литературы.