как узнать площадь параллелепипеда

Калькулятор расчета площади прямоугольного параллелепипеда

Параллелепипед — это многогранник, который представляет собой частный вид прямоугольной шестигранной призмы. В основании параллелепипеда лежит прямоугольник или равносильный ему четырехугольник, а в качестве боковых поверхностей выступают параллелограммы. Как и любая призматическая фигура, параллелепипед широко распространен в реальной жизни, но в большинстве случаев реальный многогранник принимает форму прямоугольного параллелепипеда.

Геометрия параллелепипеда

Прямоугольный параллелепипед представляет собой два одинаковых прямоугольника, лежащие в параллельных плоскостях и четыре соединяющих их прямоугольника, которые образуют боковую поверхность фигуры. В общем случае параллелепипед представляет собой частный случай прямой четырехугольной призмы. Параллелепипед — наиболее распространенная в реальной жизни фигура. Именно форму данного многогранника имеют такие объекты как дома, комнаты, кирпичи, картонные коробки, блоки компьютеров, упаковки молока, спичечные коробки и многое другое.

Реальный мир состоит их различных геометрических фигур, поэтому вам может понадобиться калькулятор, который мгновенно посчитает площадь поверхности объекта, имеющего форму прямоугольного параллелепипеда, будь то корпусная мебель, кладовка или системный блок стационарного компьютера.

Площадь поверхности параллелепипеда

Площадь полной поверхности такой призмы определяется как сумма площадей всех граней. Параллелепипед представляет собой шестигранник, каждая пара граней которого равны между собой. Это означает, что каждая грань параллелепипеда имеет свою конгруэнтную пару. Таким образом, площадь поверхности данной призматической фигуры выражается как двойная сумма площадей каждой грани.

Так как каждая грань параллелепипеда представляет собой обычный прямоугольник, то площадь одной грани определяется как произведение сторон многоугольника. Если призматическая фигура имеет стороны a, b и c, то площадь ее полной поверхности будет равна:

Для более простого понимания можем представить формулу через длину, ширину и высоту параллелепипеда. В этом случае в формуле будет лишь небольшое изменение:

Таким образом, для определения площади полной поверхности призматической фигуры вам понадобится узнать три ее параметра. Введите эти данные в форму онлайн-калькулятора и вы получите мгновенный результат. Кроме того, калькулятор сразу подсчитает длину диагонали многогранника. Расчет площади поверхности призматической фигуры может понадобиться вам во многих ситуациях.

Примеры из жизни

Покраска стен

Допустим, вы хотите покрасить стены, пол и потолок кухни белой краской. Вам необходимо купить достаточное количество краски для обработки выбранного помещения. Зная, что расход масляной краски на 1 квадратный метр поверхности составляет приблизительно 200 грамм, вы можете определить, сколько материала вам понадобится для работы. Пусть высота кухонного помещения составляет 3 м, ширина 2 м, а длина — 5 м. Введите эти данные в онлайн-калькулятор и вы получите результат в виде:

Таким образом, вам понадобится покрасить 62 квадратных метров поверхности. Для этого вам потребуется купить 12,4 кг масляной краски или 5 банок краски по 2,8 кг.

Производство

Допустим, вы работаете на производстве и покрываете стальной квадратный профиль защитным покрытием, окуная детали в ванную с раствором. Для правильного расчета параметров покраски вам необходимо знать площадь поверхности одного стального профиля, который имеет форму параллелепипеда. Стандартный квадратный профиль имеет размеры: длина 6 м, сторона а = 80 мм, сторона b = 80 мм. Для правильного расчета вам необходимо подставить все размеры в одних единицах измерения, к примеру, в сантиметрах. В этом случае вбейте в онлайн-калькулятор три стороны параллелепипеда, которые равны 600, 8 и 8. Вы получите результат в виде:

Таким образом, полная площадь поверхности стального профиля составляет 19 328 квадратных сантиметров или 1,9828 квадратных метра. Зная площадь поверхности одного профиля, вы легко сможете определить параметры покраски деталей защитным покрытием.

Заключение

Большое количество реальных объектов имеет форму параллелепипеда: это и кирпичи, и комнаты, и здания, и детали машин, и многое другое. Расчет площади данного многогранника может понадобиться в самых неожиданных ситуациях, как-то житейские проблемы или профессиональные расчеты. Наш онлайн-калькулятор поможет вам быстро определить объемы и площади поверхностей любых правильных геометрических фигур.

Источник

Полная площадь поверхности прямоугольного параллелепипеда

При изучении школьной математики часто встречаются задания, в которых требуется определить полную или боковую площадь поверхности прямоугольного или обычного параллелепипеда. Научимся это делать.

Для того, чтобы научиться вычислять площадь поверхности параллелепипеда необходимо представлять, что это такое.

Общие понятия

Изучим основные понятия. В дальнейших наших рассуждениях площадь будем обозначать латинской буквой S, угол между сторонами a и b будем обозначать как (ab).

Параллелепипедом в математике именуется четырехугольная призма, у которой все грани являются параллелограммами.

Нахождение площадей фигур

Рассмотрим, как находятся площади, могущие составлять грани параллелепипеда.

Рассмотрим на примерах как найти площадь каждой из рассматриваемых нами фигур.

1. Длина стороны квадрата равна 1600 метров. Определим его площадь.

2. Стороны прямоугольника равны 90 и 200 метров соответственно. Определим его S.

3. С параллелограммом рассмотрим два случая нахождения.

Сторона равна 300 метров, а опущенная на неё высота 250 метров. Тогда получится:

Второй вариант — стороны равны 550 и 200 метров соответственно. Угол между ними 30 градусов. Имеем:

Как видно из примеров, приведённых выше, никаких сложностей нет.

Площадь поверхности параллелепипеда

Так как наши тела имеют три принципиально различных варианта, то каждый из них мы рассмотрим в отдельности. Учтём, что полной поверхностью является сумма площадей всех граней тела, а боковой — только боковых граней.

Площадь поверхности куба

Здесь все крайне просто — грани этой фигуры равны между собой, так что S = a*a*6.

На примере это выглядит следующим образом:

Сторона равна 88 сантиметров. Площадь полной поверхности?

При данных условиях имеем:

S = a*a*6 = 88*88*6 = 46 464 сантиметра квадратного.

Площадь поверхности прямоугольного параллелепипеда

Здесь все так же довольно легко — нужно помнить, что противоположные грани равны. Таким образом, находим поверхность трёх различных граней, и каждую удваиваем. Формулы нахождения будут выглядеть следующим образом:

S = 2*(S1 + S2 + S3), где S1, S2, S3 площади всех граней соответственно.

Второй вариант S = 2*(a*b + a*c + b*c), где a, b, c соответствующие рёбра прямоугольного параллелепипеда.

Снова рассмотрим пример. Пусть рёбра прямоугольного параллелепипеда равняются 20, 30 и 40 метров. Площадь полной поверхности?

Имеем, S = 2*(a*b + a*c + b*c) = 2*(20*30 + 20*40 + 30*40) = 2*(600 + 800 + 1200) = 2*2600 = 5 200 квадратных метров.

Как видно, находить площадь прямоугольного параллелепипеда также совершенно несложно.

Поверхность параллелепипеда

Теперь рассмотрим случай когда заданное нам тело имеет вид простого параллелепипеда, его гранями являются обычные параллелограммы. Здесь, как и в предыдущем случае противоположные грани равны. Следовательно, определив поверхность трёх различных граней, мы сможем определить и полную поверхность. Значит, одна из формул опять-таки будет иметь вид:

Снова приведём пример:

В некоторых заданиях требуется определение только площади боковой поверхности параллелепипеда. В таком случае чётко указывается, что является основанием и находится только суммарная пл. четырёх боковых граней. Все приведённые выше рассуждения остаются верными.

Заключение

Тщательно изучив все сказанное выше, можно отметить, что никакой особой сложности задача по определению площади параллелепипеда не вызывает. Нужно всего-навсего чётко представлять все данные в материале математические понятия, абсолютно точно выучить формулы, ну и, разумеется, уметь хорошо проводить арифметические действия.

Видео

Из видео вы узнаете, как находить площать прямоугольного параллелепипеда.

Источник

Площадь поверхности параллелепипеда: онлайн-калькулятор

Для нахождения площади полной поверхности параллелепипеда необходимо рассчитать сумму площадей трех его граней и удвоить результат. Чтобы не совершать действия вручную и получить верный ответ быстро, воспользуйтесь нашим сервисом.

Наша компания помогает разобраться в задачах по алгебре и геометрии. Сервис работает без регистрации и оплаты. Автоматизированная программа производит последовательные вычисления, которые доступны для просмотра. Такая система позволяет избежать ошибок во время промежуточных действий.

Вычисление площади поверхности параллелепипеда. Онлайн-калькулятор

В программу заложен расчет площади поверхности параллелепипеда по формуле:

где a, b, h – ребра фигуры.

Для школьников сервис с основными математическими вычислениями – это возможность самостоятельно подготовиться к поступлению в ВУЗ. Число запросов на расчет не ограничивается, поэтому тренироваться в решении задач можно до полного усвоения темы. Формула в решении в совокупности с готовым чертежом ускоряет запоминание материала. Совершение вычислений не требуется оплачивать. Бесплатная помощь ученикам позволяет сэкономить на репетиторах и повысить успеваемость по математике.

Также сервис используют:

В разделе калькуляторов вы также найдете программы для нахождения площадей других фигур. ​​​​​​​

Источник

Площадь поверхности прямоугольного параллелепипеда – формула (5 класс, математика)

В 5 классе в курсе математики изучается тема прямоугольного параллелепипеда. Сегодня мы поговорим о формулах для нахождения площади прямоугольного параллелепипеда боковой поверхности и площади полной поверхности этой фигуры, которые наиболее часто вызывают затруднение у учеников при изучении этой темы.

Определения

Параллелепипед – это фигура, который состоит из шести четырехугольников. Если в основании этой фигуры находится прямоугольник, то многогранник называется прямоугольным параллелепипедом.

Прямоугольный параллелепипед имеет четыре боковые грани. Две из них называются основанием многогранника. Для обозначения вершин фигуры используют большие латинские буквы.

Если две грани не имеют общего ребра, то они называются противоположными. Так как каждая грань является прямоугольником, где противоположные стороны равны, то и противоположные грани прямоугольного параллелепипеда равны.

Стороны граней – это ребра, фигура имеет 12 ребер. Длина ребер определяет основные характеристики прямоугольного параллелепипеда: площадь, периметр, объем.

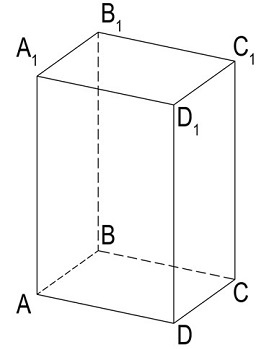
Рис. 1. Прямоугольный параллелепипед

Примеры таких фигур мы часто встречаем в нашей жизни: кирпич, коробка, системный блок компьютера.

Математическая фигура – прямоугольный параллелепипед активно используется в искусстве, архитектуре и прочих областях.

Различают несколько видов параллелепипедов, с основанием в виде квадрата, параллелограмма или прямоугольника.

Формула для нахождения площади

Для того, чтобы найти площадь боковой поверхности прямоугольного параллелепипеда, необходимо вычислить по отдельности площадь каждой боковой грани, а затем просуммировать получившиеся значения.

$S = ac, a, b, c$ – стороны фигуры.

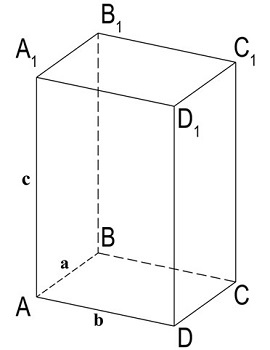
Рис. 2. Прямоугольный параллелепипед

Соответственно, чтобы вычислить площадь полной поверхности прямоугольного параллелепипеда необходимо сложить площадь боковой поверхности и две площади основания. В итоге получится формула площади прямоугольного параллелепипеда.

$S = 2(ab + ac) + 2 bc = 2(ab + ac + bc)$

Иногда для уточнения возле знака площади пишут краткое обозначение например, S п.п – площадь полной поверхности, либо S б.п – площадь боковой поверхности. Это помогает вовремя выполнения задание не перепутать нужные данные.

Пример задания

Найти площадь полной поверхности прямоугольного параллелепипеда, если длина и ширина основания 4 см и 3 см соответственно, а высота равна 2 см.

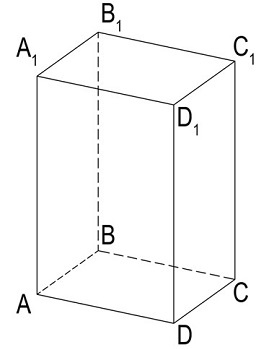
Рис. 3. Прямоугольный параллелепипед со сторонами a, b, c

Решение:

S п.п. = 2(4 * 3 + 4*2 + 3*2) = 52 см2

Таким образом, S п.п. = 52 см2.

Для площади поверхности прямоугольного параллелепипеда используют те же единицы измерения, в которых были приведены длины ребер. При необходимости их нужно перевести в единую систему измерения.

Что мы узнали?

Мы познакомились с элементами прямоугольного параллелепипеда: грани, ребра, основание. А также ознакомились с формулами для нахождения площади боковой и полной поверхности многоугольника, которые можно использовать для решения заданий.

Источник

Площадь поверхности параллелепипеда

Что такое площадь поверхности параллелепипеда

Параллелепипед — четырехугольная призма, основаниями которой являются параллелограммы. Частный случай этой геометрической фигуры — прямой параллелепипед, у которого все грани являются прямоугольниками.

В общем случае площадь — это численное значение, характеризующее размер двумерной геометрической фигуры.

Параллелепипед может существовать только в трех измерениях, поэтому для него вводится понятие площади поверхности. В геометрическом смысле площадь поверхности объемной фигуры является совокупностью площадей ее граней.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Формула нахождения полной площади

В задачах чаще всего имеется дело с прямоугольным параллелепипедом. Для него полная площадь поверхности вычисляется следующим образом:

\(S=2\cdot(a\cdot b+a\cdot c+b\cdot c)\)

где a, b и c — длины ребер, исходящих из любой вершины параллелепипеда.

Рассмотрим то, как данная формула выводится. Как уже упоминалось выше, площадь поверхности объемной фигуры является совокупностью площадей ее граней. Для наглядности возьмем параллелепипед ABCDA₁B₁C₁D₁.

Полная площадь его поверхности равняется сумме площадей всех граней: \(S_<пар>=S_+S_+S_+S_+S_+S_\)

Согласно свойствам параллелепипеда, его противоположные грани равны между собой. Следовательно, нет необходимости вычислять площадь всех шести граней, можно ограничиться тремя, а затем их сумму умножить на 2:

Грани прямого параллелепипеда являются прямоугольниками. Площадь данной фигуры равняется произведению ее сторон:

У выбранных нами для расчета площади граней есть три общие стороны: AB, AD и AA₁. Для удобства обозначим их как a, b и c соответственно.

Подставим данные значения в обозначенную выше формулу площади параллелепипеда:

\(S_<пар>=2\cdot\left(a\cdot b+a\cdot c+b\cdot c\right)\)

Вычисление площади боковой поверхности прямоугольного параллелепипеда

Кроме полной площади поверхности, в расчетах иногда необходимо вычислить площадь боковой поверхности, то есть совокупность площадей боковых граней, без учета оснований.

Для этого есть три взаимосвязанные формулы:

Примеры решения задач

Задача

Вычислить полную площадь поверхности прямоугольного параллелепипеда ABCDA₁B₁C₁D₁.

Дано: AB = 3, A₁B = 6, AD = 5.

Решение

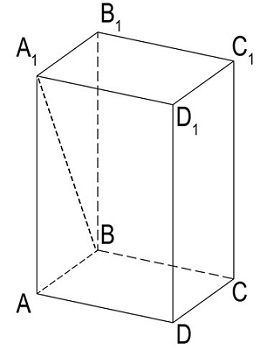
Для расчета полной площади необходимо знать длины трех сторон. В данном случае нам понадобится вычислить длину стороны AA₁. Так как длина диагонали A₁B известна, сделать это нетрудно.

Воспользуемся теоремой Пифагора:

Подставим известные значения в формулу расчета площади поверхности:

\(S=2\cdot(a\cdot b+a\cdot c+b\cdot c)\)

\(S=2\cdot(AB\cdot AD+AB\cdot AA_1+AD\cdot AA_1)=2\cdot(3\cdot5+3\cdot5+5\cdot5)=2\cdot(15+15+25)=2\cdot55=110\)

Задача 2

Вычислить длину стороны прямого параллелепипеда ABCDA₁B₁C₁D₁.

Решение

Так как нам известна одна из сторон основания — b а в основании параллелепипеда лежит прямоугольник, найти вторую сторону проще всего будет через площадь этого основания:

Отличие площади боковой поверхности от полной в том, что в ней не учитываются нижняя и верхняя грани фигуры. Следовательно, их разность будет равняться двум площадям основания. Вычислим это значение:

\(S_<пов>-S_<бок>=2\cdot a\cdot b+2\cdot a\cdot c+2\cdot b\cdot c-2\cdot a\cdot c-2\cdot b\cdot c=2\cdot a\cdot b\)

Преобразуем выражение так, чтобы вычислить длину неизвестной стороны:

Источник