как узнать радиус скругления детали
Радиусы скруглений. Размеры и предельные отклонения
Источник: ОСТ 92-0093-69
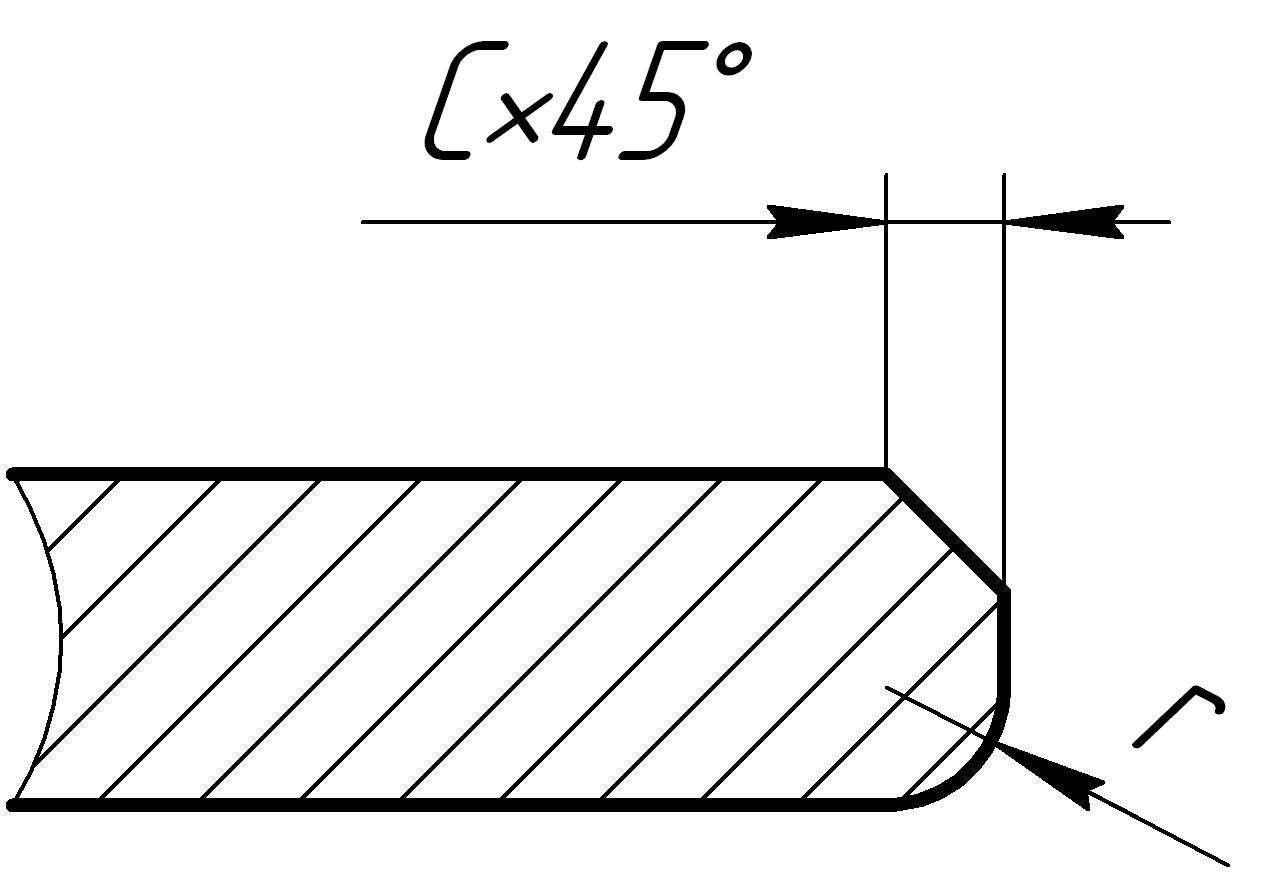
Рис 1. Размеры и предельные отклонения радиусов скруглений и фасок для сопряжений типа «вал – отверстие»
Таблица 1. Рекомендуемый подбор сопряжений радиуса с радиусом и радиуса с фаской, мм
Таблица 2. Размеры и предельные отклонения радиусов скруглений или фасок для сопрягаемых поверхностей валов и втулок, мм
При применении радиусов скруглений или фасок размером св. 6 до 10 мм предельное отклонение ±1,5 мм; св. 10 до 20 – ±2 мм; св. 20 до 32 – ±2,5 мм и свыше 32 – ±3 мм.
Таб 3. и Рис.2 Размеры и предельные отклонения радиусов скруглений валов и корпусов, сопрягаемых с шарико- и роликоподшипниками, мм
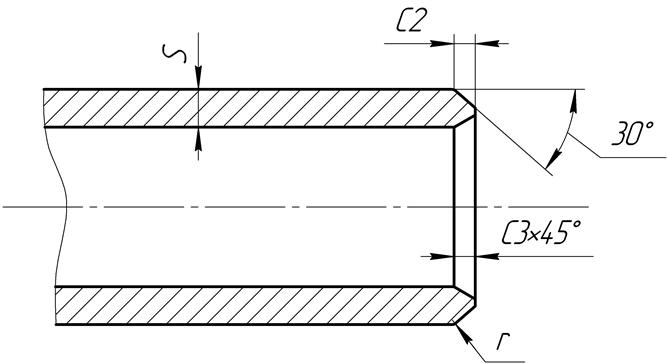
Рис 3. и Таб 4. Размеры фасок и радиусов и предельные отклонения на механически обрабатываемые плоские детали
Рис. 4 и Таб. 5. Размеры и предельные отклонения фасок на валах под запрессовку
Таб. 6
Рис. 5 и Таб.7. Размеры и предельные отклонения фасок на втулках под запрессовку
Примечание: величину радиуса скругления и предельные отклонения на него выбирать по таблице 5.
Размеры радиусов и фасок сопрягаемых поверхностей типа «вал – отверстие», валов и корпусов с шарико- и роликоподшипниками, а также валов и втулок под запрессовки, должны быть указаны в чертежах с числовыми значениями предельных отклонений.
Размеры радиусов скруглений и фасок несопрягаемых поверхностей валов и втулок и размеры фасок и радиусов на плоских деталях должны быть указаны в чертежах. Предельные отклонения этих размеров на изображении не наносятся, а в технических требованиях чертежа пишется: «Неуказанные предельные отклонения размеров радиусов и фасок по ОСТ 92-0093-69».
Предельные отклонения на угловые размеры фасок ± 3°.
К оглавлению
Главконструктор работает с компаниями в городах:
Санкт-Петербург, Москва, Севастополь, Воронеж, вся Россия.
Радиусы скруглений. Размеры и предельные отклонения
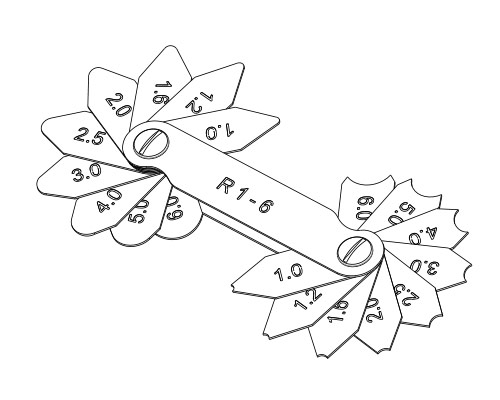
Радиусомер шаблонный
Радиус закруглений и галтелей измеряется с помощью радиусомера, представляющего собой набор шаблонов в виде пластин. С обоймой все шаблоны соединены с помощью шарниров. Это точный, надежный и простой в использовании инструмент, позволяющий быстро произвести все необходимые замеры.
При измерении радиуса закруглений детали нужно приложить к ее поверхности шаблон радиусомера и просмотреть на просвет место, в котором они между собой соприкасаются. На шаблоне указано число, определяющее величину радиуса закругления детали, при котором отсутствует зазор между поверхностью детали и шаблоном.
Повышение прочности деталей
Для того, чтобы в значительной мере повысить усталостную прочность поверхности нужно увеличить плавность переходов, между ступенчатыми поверхностями деталей, применив для этой цели галтели.
Повышение усталостной прочности достигается также при помощи поверхностной термической обработки деталей, улучшения качества обработки деталей и упрочнения различных поверхностей пластическим деформированием.
По своей форме галтели – это скругления как внешних, так и внутренних деталей машин, помогающие значительно облегчить процесс изготовления деталей ковкой, литьем и штамповкой. Их можно увидеть в различных механизмах и узлах. Скругления повышают также прочность характеристик валов и осей в местах, где осуществляется переход от одного диаметра к другому.
Обтекаемые формы галтелей сокращают концентрацию напряжения в поверхностях деталей, делают их более прочными, надежными и долговечными. Поэтому на производстве скругления – это оптимальный элемент, повышающий усталостную прочность поверхностей.
Обтачивание скруглений
Обтачивание галтелей или скруглений различных деталей выполняется с помощью токарной обработки при помощи вращения детали. Это одна из древних механизированных операций по обработке различных деталей. Используется токарный станок и резец.
Внутреннее и наружное резание выполняется резцом во время вращения поверхностей. Качество обработки зависит от резца, металла из которого сделана обрабатываемая деталь и самого токарного станка. Вращением обрабатываемой детали могут быть обработаны фасонные поверхности многих тел, т. е. применяются те же способы, что и при обработке конических и цилиндрических поверхностей.
Для обтачивания скруглений применяются проходные резцы с закруглениями с соответствующим радиусом, используя поперечную или продольную подачу. Все замеры в процессе токарной обработки и окончательные формы детали измеряются и контролируются измерительным инструментом и в частности с помощью радиусомера.
Конструирование отливок
Конструирование отливок на производстве предусматривает максимальное снижение их массы и упрощение конструкции. Механическая обработка сводится к минимуму. Технологии литья влияют на формообразование отливок.
Выбор формообразования рациональных элементов отливок (переходов, сопряжений, ребер жесткости, скруглений и т. д.), в первую очередь, диктуется желанием получить достаточно жесткую и качественную отливку. Это касается всех известных сегодня методов формообразования.
Для получения удобной в работе отливки конструктору необходимо особое внимание уделять надлежащей литейной форме и правильности оформления переходов.
Качественные литейные формы, в которых учитывается технологический уклон, радиус скругления, жесткость ребер и т. д., можно получить, соединив возможности станков с числовым программным управлением и автоматизированного проектирования.
Как померить радиус скругления?
Как измерить радиус скругления на детали?
Измерение радиусов закруглений. Радиусы закруглений измеряют набором радиусомеров. При отсутствии ради-усомеров радиусы можно определить по оттискам на бумаге. Для этого необходимо кусочек бумаги наложить на измеряемый участок и нажать твердым предметом или постучать по бумаге, прижатой к кромке детали.
Как измерить радиус на детали?
Измерить радиус можно просто: отмечаем стартовое положение одного колеса (наружного), выворачиваем до конца рулевое колесо, разворачиваемся на полные 180 градусов, отмечаем конечное положение того же колеса. Между отметками замеряем расстояние, половина его и будет радиусом разворота.
Как в компасе сделать радиус скругления?
Команды Фаска, Скругление находятся на инструментальной панели Редактирование детали. В Главном меню: Операции->Фаска/Скругление. Эта команда применяется для построения фаски или скругления на ребре детали.
Что такое радиус скругления?
2.5 радиус скругления: Радиус дуги окружности, которая наиболее близка к закругленной форме рассматриваемого элемента.
Как правильно измерить расстояние между отверстиями?
Расстояние между центрами можно определить при помощи нутромера или линейки. Измеряют расстояние между кромками отверстий l1 или l2. Результаты в обоих случаях будут одинаковыми. l = l1 + (d — d1)/2 = 36 + (20 — 8)2 = 42 мм.
Как правильно измерить радиус?
Радиус круга рассчитывается по следующим формулам:
Как правильно указать радиус на чертеже?
Как измерить диаметр?
Следовательно, для того, чтобы измерить диаметр трубы, понадобится значение C (длина окружности) разделить на 3,14.
…
Как можно измерить диаметр подручными приспособлениями
Чем можно измерить радиус?
Радиус обозначается буквой «R» и измеряется в метрах.
Как сделать фаски в компасе?
Чтобы построить фаску на объекте 1,6х45 градусов нужно на Панели Свойств задать тип построения фаски — Фаска по длине и углу (на рисунке), указать длину фаски 1,6 мм и угол фаски 45 градусов. Также проследите, чтобы первый и второй элементы усекались (чтобы не оставались линии) и не создавалось условное пересечение.
Как определить радиус дуги?
Основные формулы окружности:
Как правильно закруглить углы?
Чтобы правильно закруглить, отмеряем на стежке высоту свеса с каждой стороны угла и отмечаем точку пересечения этих высот. Затем из этой точки чертим дугу радиусом, равным высоте свеса покрывала. Лишнее отрезаем. Так же отрезаем припуск на подгибку, начиная и заканчивая в месте начала скругления.
Как определить радиус дуги или сегмента круга и найти центр
Первый метод определения радиуса дуги или сегмента круга
Изначально это выглядит так:
Рисунок 463.1. а) имеющаяся дуга, б) определение длины хорды сегмента и высоты.
Таким образом, когда имеется дуга, мы можем соединить ее концы и получим хорду длиной L. Посредине хорды мы можем провести линию, перпендикулярную хорде и таким образом получим высоту сегмента H. Теперь, зная длину хорды и высоту сегмента, мы можем сначала определить центральный угол α, т.е. угол между радиусами, проведенными из начала и конца сегмента (на рисунке 463.1 не показаны), а затем и радиус окружности.
Решение подобной задачи достаточно подробно рассматривалось в статье «Расчет арочной перемычки», поэтому здесь лишь приведу основные формулы:
Как видим, с точки зрения математики никаких проблем с определением радиуса окружности нет. Данный метод позволяет определить значение радиуса дуги с любой возможной точностью. Это главное достоинство данного метода.
А теперь поговорим о недостатках.
Кроме того, для того, чтобы найти центр окружности, нужно продлить высоту сегмента и отложить на этой прямой расстояние, равное радиусу. Так как на практике мы имеем дело с не идеальными измерительными приборами, к этому следует прибавить возможную погрешность при разметке, то получается, что чем меньше высота сегмента по отношению к длине хорды, тем больше может набежать погрешность при определении центра дуги.
Опять же не следует забывать о том, что мы рассматриваем не идеальный случай, т.е. это мы так сходу назвали кривую дугой. В действительности это может быть кривая, описываемая достаточно сложной математической зависимостью. А потому найденный таким образом радиус и центр окружности могут и не совпадать с фактическим центром.
В связи с этим я хочу предложить еще один способ определения радиуса окружности, которым сам часто пользуюсь, потому что этим способом определить радиус окружности намного быстрее и проще, хотя точность при этом значительно меньше.
Второй метод определения радиуса дуги (метод последовательных приближений)
Итак продолжим рассмотрение имеющейся ситуации.
Так как нам все равно необходимо найти центр окружности, то для начала мы из точек, соответствующих началу и концу дуги, проведем как минимум две дуги произвольного радиуса. Через пересечение этих дуг будет проходить прямая, на которой и находится центр искомой окружности.
Теперь нужно соединить пересечение дуг с серединой хорды. Впрочем, если мы из указанных точек проведем не по одной дуге, а по две, то данная прямая будет проходить через пересечение этих дуг и тогда искать середину хорды вовсе не обязательно.
Ну а дальше все просто: измеряем расстояние от пересечения дуг до начала (или конца) рассматриваемой дуги, а затем расстояние от пересечения дуг до точки, соответствующей высоте сегмента.
Исходя из этого на прямой принимается следующая точка, предположительно соответствующая центру дуги, и от нее производятся те же измерения. Затем принимается следующая точка и измерения повторяются. С каждой новой точкой разница измерений будет все меньше.
Вот собственно и все. Не смотря на столь пространное и мудреное описание, для определения радиуса дуги таким способом с точностью до 1 мм достаточно 1-2 минут.
Теоретически это выглядит примерно так:
Рисунок 463.2. Определение центра дуги методом последовательных приближений.
А на практике примерно так:
Фотография 463.1. Разметка заготовки сложной формы с разными радиусами.
Тут только добавлю, что иногда приходится находить и чертить несколько радиусов, потому на фотографии так много всего и намешано.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Я достаточно подробно ответил на ваш вопрос в статье «Расчет арочной перемычки», где вы задали подобный вопрос.
Сначала термины:
Отрезок, соединяющий концы дуги называется хордой (a), а высота сегмента (перпендикуляр из середины хорды) — стрелкой (h).
Теорема Пифагора: Квадрат гипотенузы равен сумме квадратов катетов. То есть R^2=(R-h)^2+(a/2)^2.
А что касается нахождения центра, то перпендикуляры к серединам хорд пересекаются в центре!
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).
Простая формула для определения радиуса дуги
Полезно знать математический способ, позволяющий рассчитать радиус дуги. Он особенно удобен, когда требуется точно разметить плавную дугу с помощью большого импровизированного циркуля, а не гибкого лекала, после того как вам стали известны три опорные точки или два главных размера.

Например, если нужно построить дугу длиной 240 и высотой 30 мм, следует действовать так:
Сначала подставьте эти размеры в формулу. В нашем случае L=120, Н=30, поэтому (1202+302): (2×30) = (14400+900): 60= 153000:60 = 255.
Теперь сделайте для этого радиуса циркуль, как показано на фото внизу. Выровняйте один конец с серединой дуги на заготовке. Проведите из этой точки под прямым углом по линейке прямую линию и поставьте на нее второй конец циркуля. Теперь вы можете начертить идеальную дугу, которая соединит все три опорные точки.